- Банк заданий
- Математика (профиль)
- Задание 60227
Задание №60227 ЕГЭ по Математике (профиль)
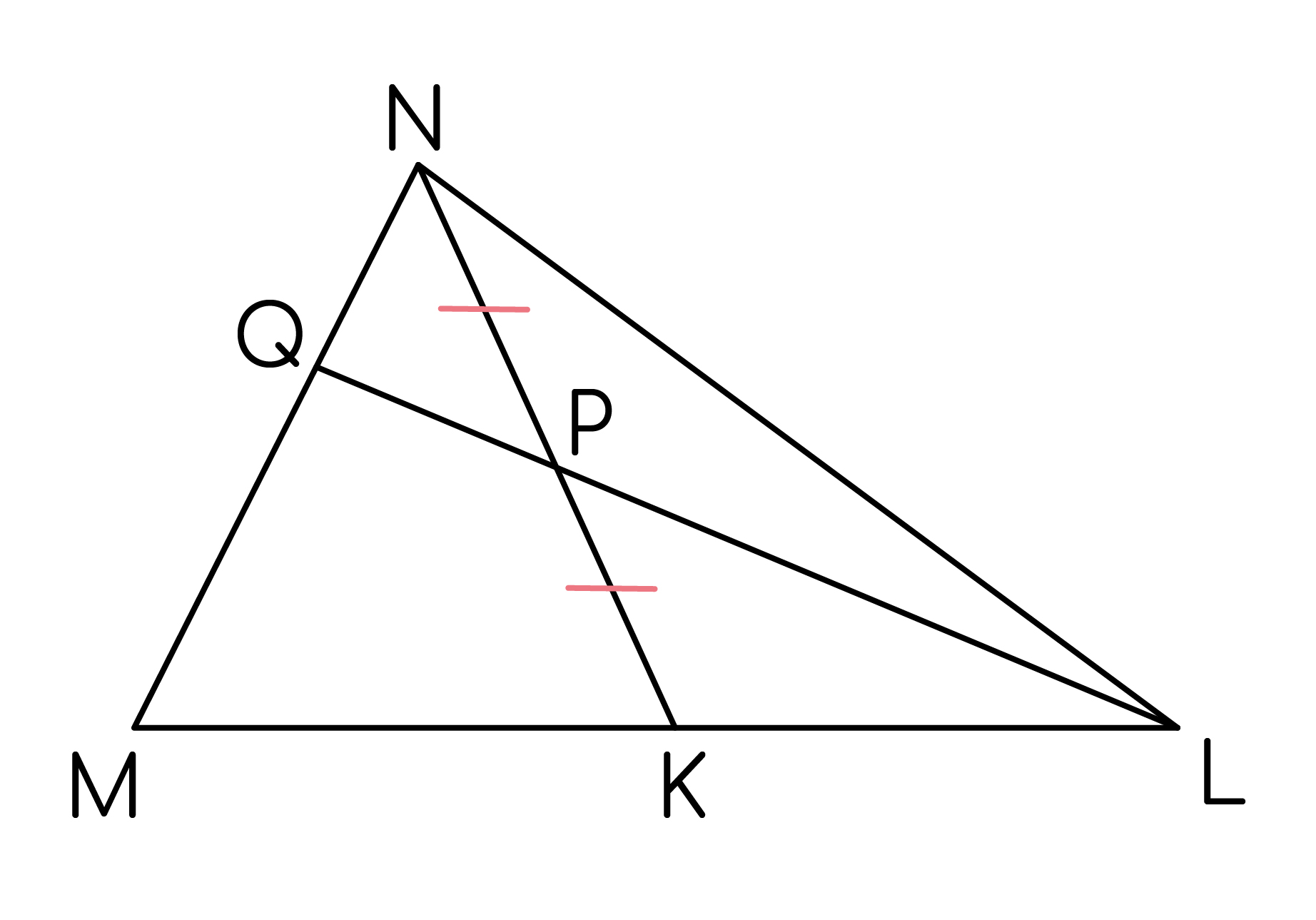
Дан остроугольный треугольник MNK, на середине его стороны NK отмечена c точка Р, а на стороне MN - точка Q так, что 
Прямая QP пересекает продолжение стороны MK в точке L.
а) Докажите, что 
б) Найдите площадь треугольника NKL, если известно, что 
Решение:
а) Воспользуемся теоремой Менелая для △MNK: 
Подставив отношения из условия, получим 
Значит, 
б) 
тогда NK - медиана, и 
Так как P - середина NK, то 
Воспользуемся теоремой косинусов для △MNK: 
Найдем площадь △MNK:
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов
Ответ: б) 
Источник: NeoFamily