Задание №47770 ЕГЭ по Математике (профиль)

Решение:

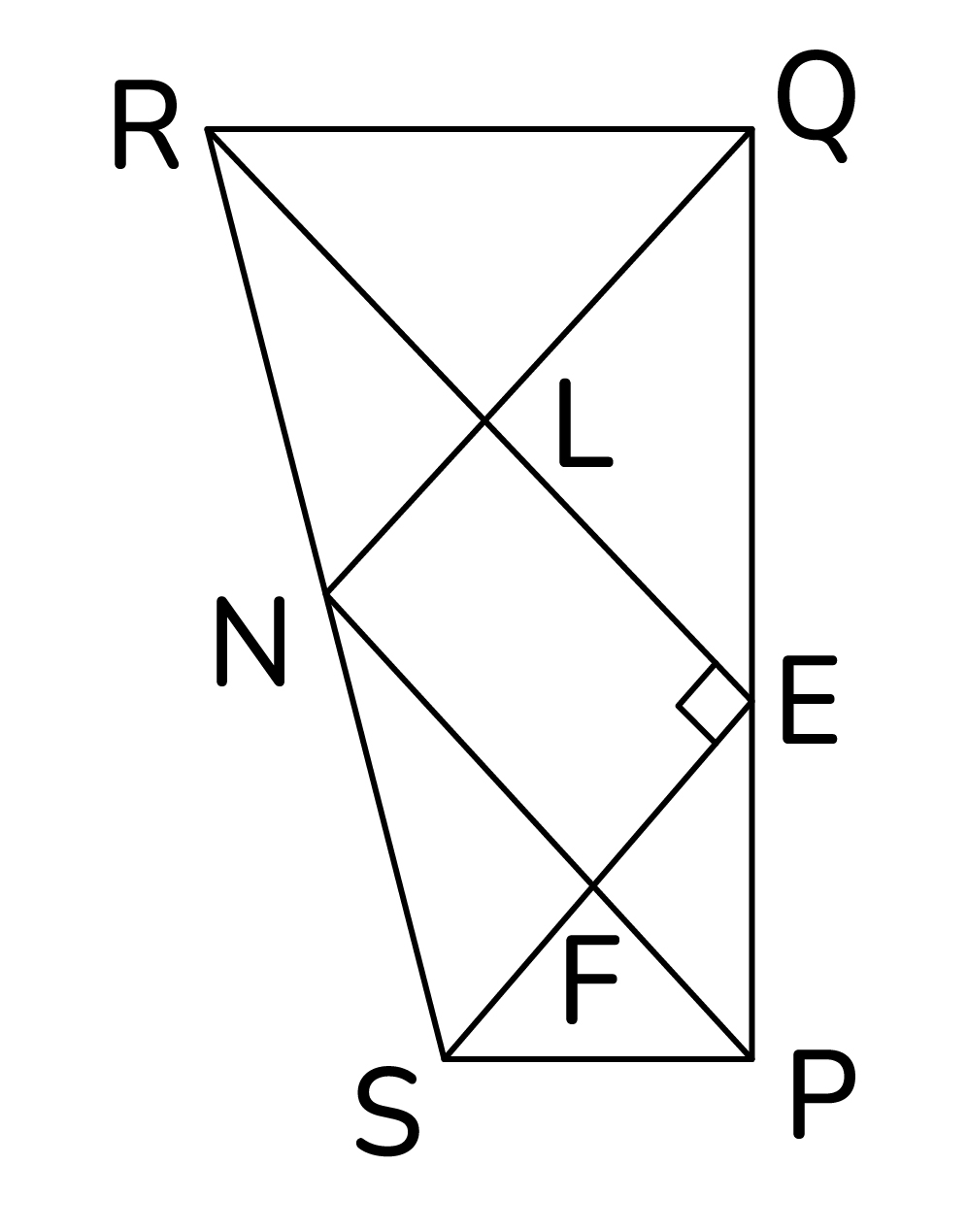
а) Так как то равнобедренные. Пусть L - точка пересечения биссектрисы F - биссектрисы  и SE. Тогда QL и PF - медианы, высоты  соответственно. Так как то Тогда прямая PF пересекает SR в точке N, где N - середина SR. Аналогично,  тоже пересекает SR посередине, то есть в точке N, значит,  в точке N, которая лежит на стороне SR.

б) Запишем площадь SPQR как сумму площадей треугольников, из которых он состоит:  Они все прямоугольные.
1) 
2) равнобедренный, значит, Тогда  
3) Аналогично, равнобедренный, и  и 
Тогда 

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов

Ответ: б) 

Источник: NeoFamily