- Банк заданий
- Математика (профиль)
- Задание 47766
Задание №47766 ЕГЭ по Математике (профиль)
Существует такой треугольник MNK, что и вокруг него описана окружность, и в него вписана окружность, но уже с центром в точке Q. Прямая NQ второй раз пересекает окружность в точке R.
а) Приведите доказательства того, что треугольник RQK равнобедренный
б) Вычислите площадь треугольника MRK, если известно что радиус описанной окружности равен 14, а 
Решение:
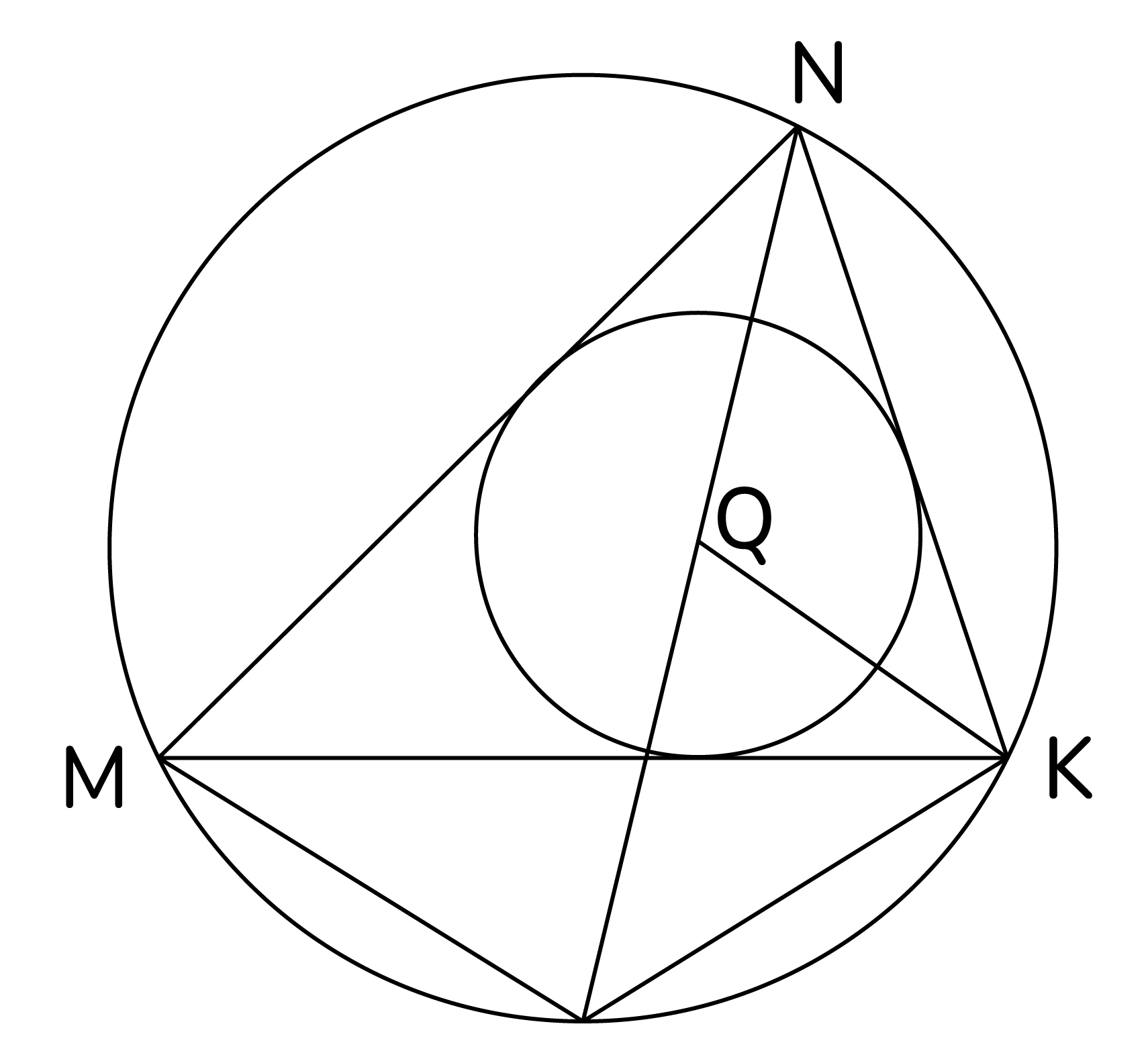
а) Используем точку Q как центр вписанной в треугольник окружности: в треугольнике MNK отрезки NQ и KQ являются биссектрисами. И так как они делят свои углы пополам, то справедливо будет и следующее: 
так как они опираются на одну и ту же дугу окружности, описанной около треугольника MNK, поэтому составим следующее уравнение: 
Таким образом, и треугольник RQK является равнобедренным.
б) Заметим, что хорды MR и KR стягивают равные дуги окружности, следовательно: 
Таким образом, 
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов
Ответ: б) 
Источник: NeoFamily