- Банк заданий
- Математика (профиль)
- Задание 47756
Задание №47756 ЕГЭ по Математике (профиль)
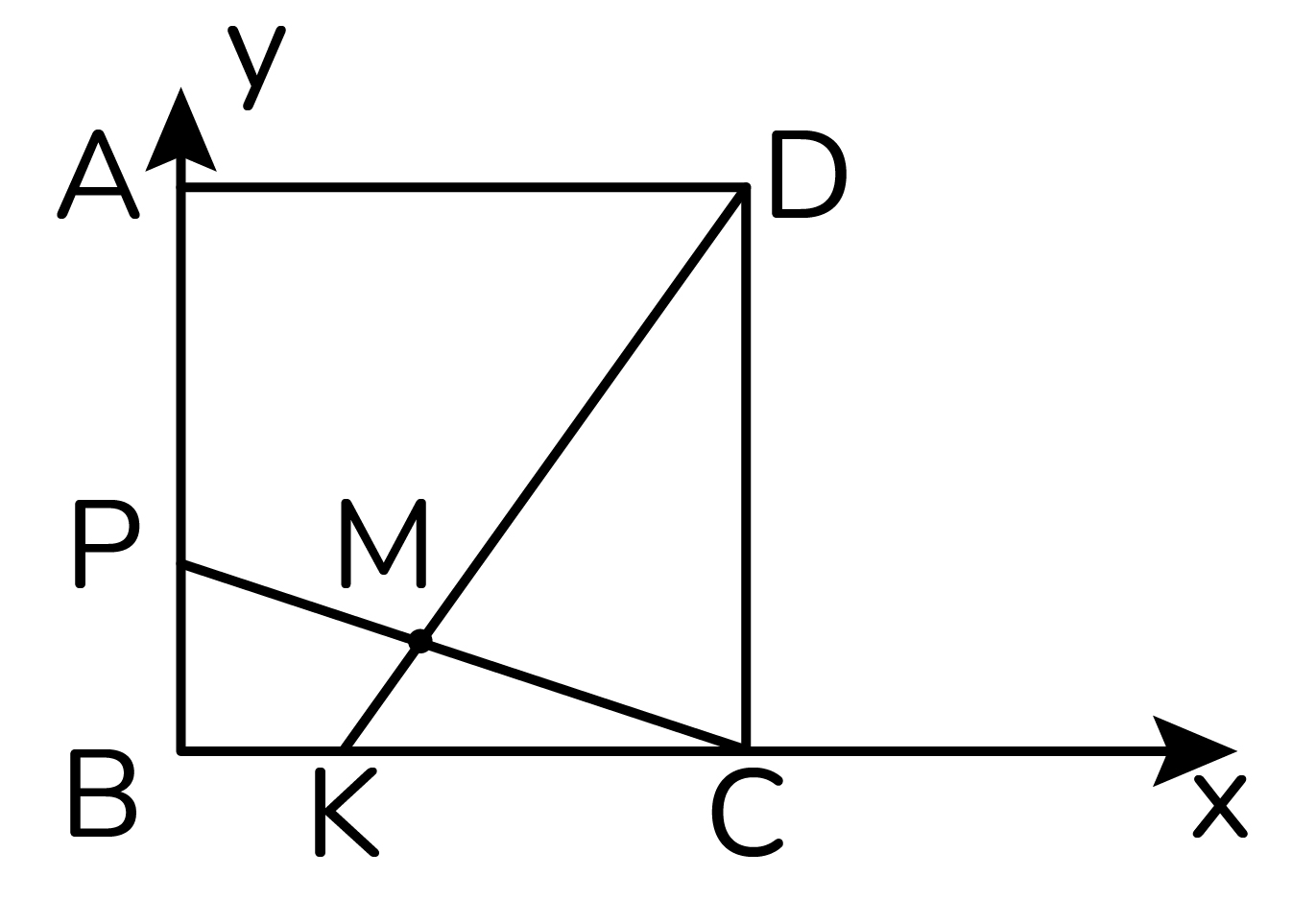
Из вершин C и D прямоугольника ABCD опущены прямые, пересекающие стороны AB и BC соответственно в точках P и K, причем 
а) Докажите, что если 
то 
б) Найдите отношение длин отрезков CM и PM, где M – это точка пересечения CP и DK.
Решение:
а) Так как 
то ABCD - квадрат. Пусть сторона квадрата имеет длину 16. Удобно ввести такую систему координат (см. рисунок): P(0; 4), K(3; 0), D(16; 16), C(16; 0). Уравнения прямых можно выяснить по общей формуле: 
Вычислим косинусы 
и 
Значит, 
б) Решим систему уравнений:
Тогда 
поэтому 
Значит, 
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов
Ответ: б) 
Источник: NeoFamily