Задание №47754 ЕГЭ по Математике (профиль)

Решение:

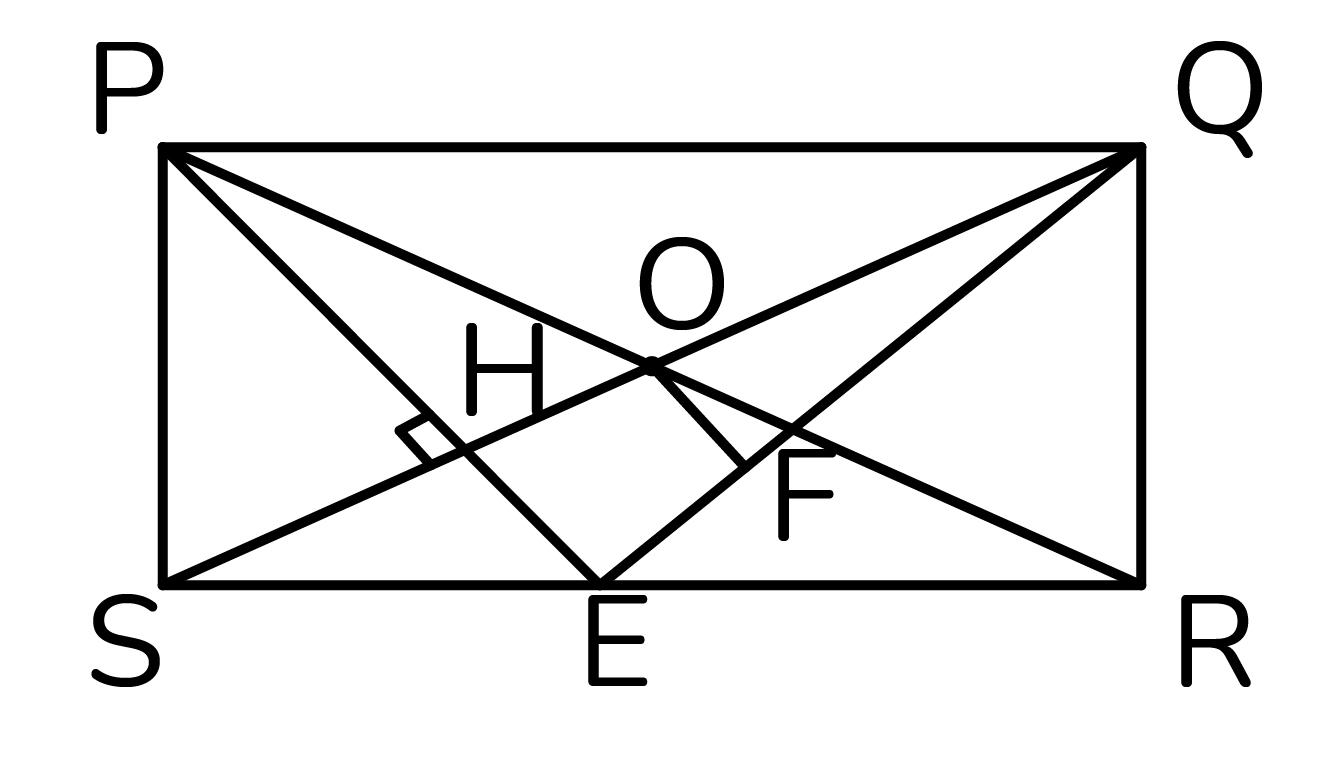
а) Так как  то SPQR - прямоугольник. Обозначим  равнобедренный, поэтому   как прямоугольные треугольники по катету и гипотенузе, поэтому  Пусть Н - точка пересечения PE и SQ. Тогда РН - высота прямоугольного треугольника SPQ, проведенная из вершины прямого угла. Значит, 

б) Имеем 

Из прямоугольного треугольника QER находим 
Пусть О - центр SPQR, OF - расстояние до QE, OF - высота QEO.

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов

Ответ: б) 

Источник: NeoFamily