Задание №47758 ЕГЭ по Математике (профиль)

Решение:

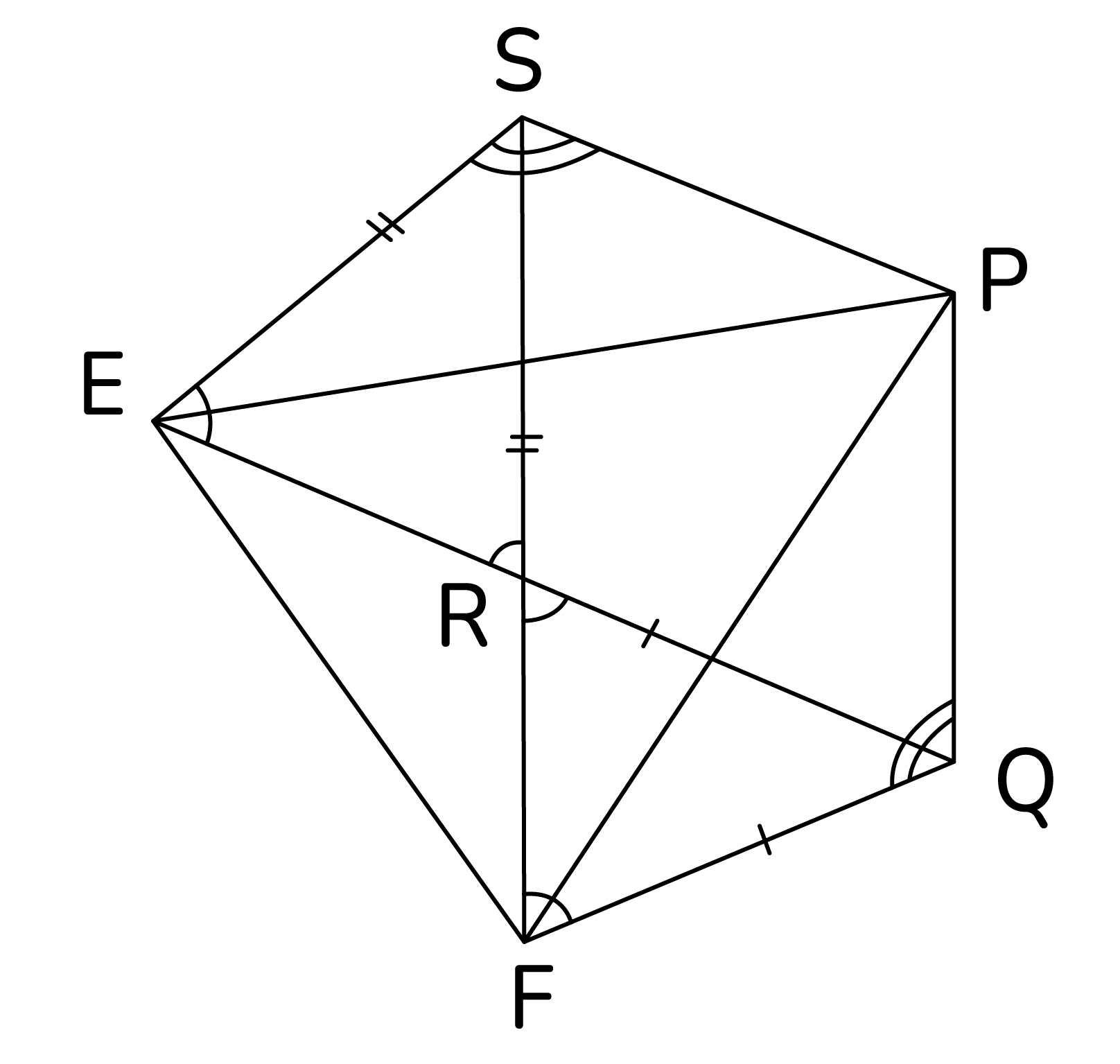
а) Так как противоположные стороны SPQR параллельны, то SPQR - параллелограмм. Так как равнобедренный, то Аналогично, равнобедренный,  и вертикальные, значит  Так как SPQR - параллелограмм, то  и Но тогда 

б) Так как отрезок EF виден из точек S и Q под равными углами, то точки S, P, Q, R лежат на одной окружности. Тогда вписанный и справделиво равенство:  Имеем:  Откуда находим 

Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов

Ответ: б) 

Источник: NeoFamily