- Банк заданий
- Математика (профиль)
- Задание 38466
Задание №38466 ЕГЭ по Математике (профиль)
В трапеции ABCD основание AD в два раза меньше основания BC. Внутри трапеции взяли точку М так, что углы ВАМ и CDM прямые.
а) Докажите, что ВМ = СМ.
б) Найдите угол АВС, если угол BCD равен 64°, а расстояние от точки М до прямой ВС равно стороне AD.
Решение:
а) Пусть прямые 
и 
пересекаются в точке 
Тогда треугольники 
и 
подобны с коэффициентом подобия 2, поскольку 
Значит, 
и 
- середины 
и 
соответственно. Таким образом, 
и 
- серединные перпендикуляры в треугольнике 
а 
- центр описанной около этого треугольника окружности, поэтому 
как радиусы этой окружности.
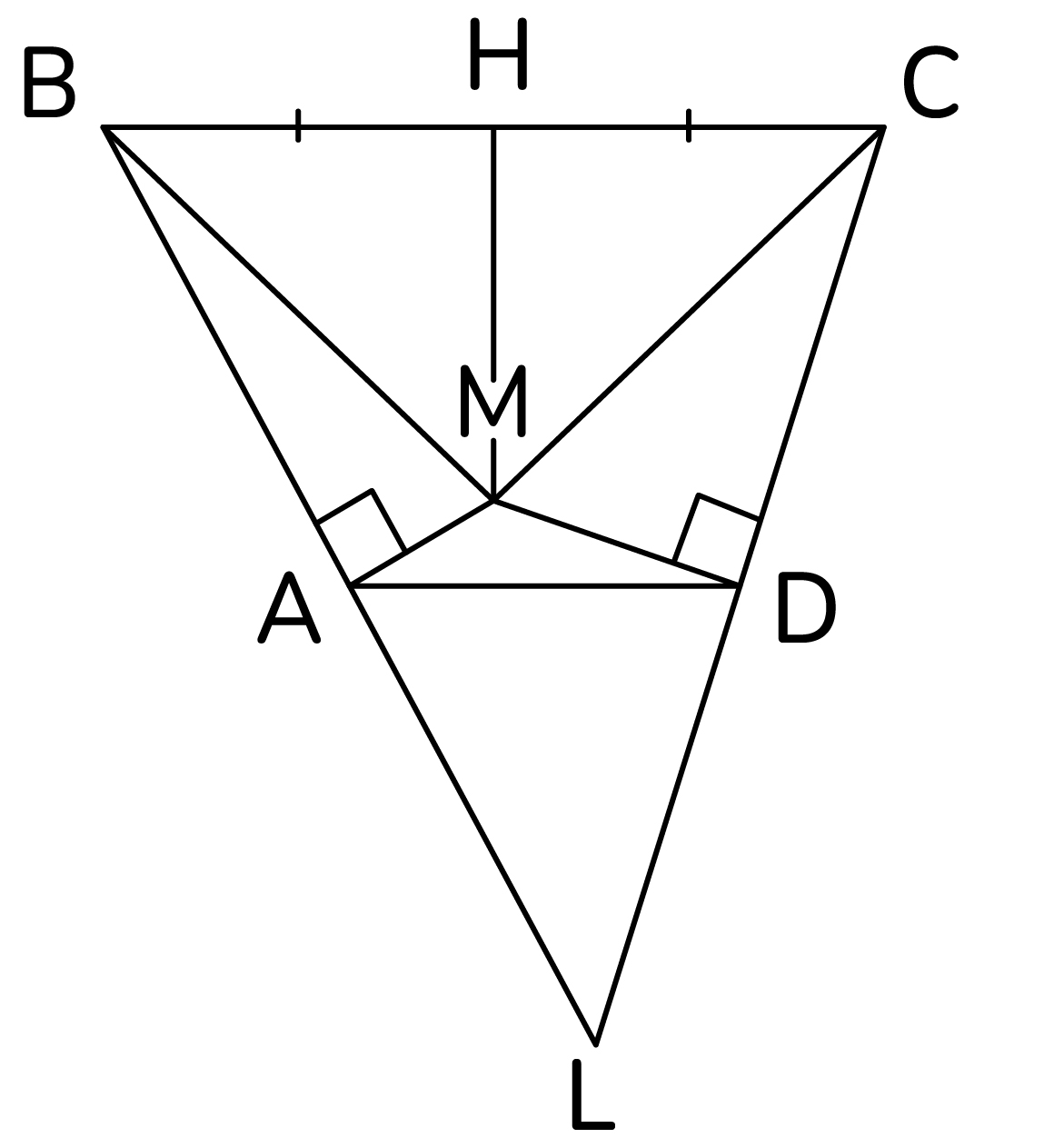
б) Пусть 
- середина 
тогда 
- серединный перпендикуляр к стороне ВС. Значит, треугольники 
и 
равнобедренные прямоугольные, поэтому 
По свойству вписанного угла 
откуда 
Имеется верное доказательство утверждения пункта a) и обоснованно получен верный ответ в пункте б) - 3 балла
Получен обоснованный ответ в пункте б) ИЛИ имеется верное доказательство утверждения пункта а) и при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки - 2 балла
Имеется верное доказательство утверждения пункта а), ИЛИ при обоснованном решении пункта б) получен неверный ответ из-за арифметической ошибки, ИЛИ обоснованно получен верный ответ в пункте б) с использованием утверждения пункта а), при этом пункт а) не выполнен - 1 балл
Решение не соответствует ни одному из критериев, приведённых выше - 0 баллов
Ответ: б) 71°
Источник: Реальные задания (ЕГЭ, ФИПИ, Ященко)