Задание №62180 ЕГЭ по Математике (профиль)

Решение:
Разложим неравенство на множители:

В уравнении раскроем второй квадрат и преобразуем:


поэтому гарантированно 
Теперь в неравенстве обратим внимание на скобку  Так как  эта скобка положительная. Поэтому на нее можно сократить. Сделаем это и подставим 

Решим неравенство:


Получили систему:

Изобразим её в координатах  Это кусочек параболы  с вершиной  определённый при 

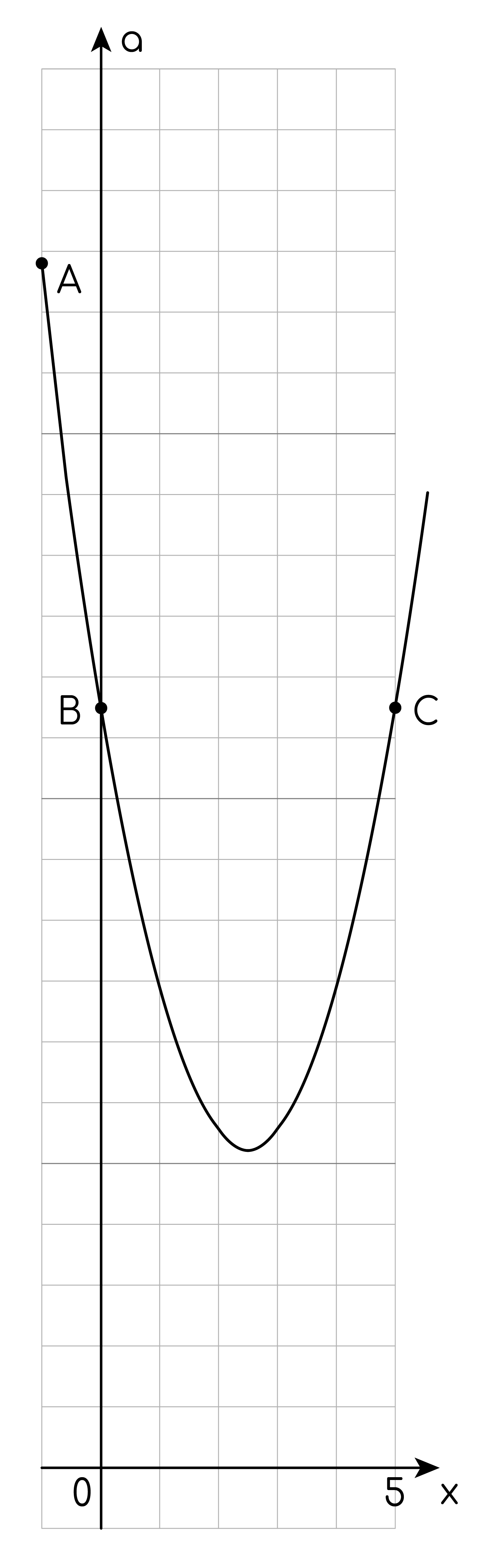
Отметим на чертеже точку  где парабола пересекает прямую  точку  где парабола пересекает прямую  и точку  на параболе с той же -координатой, что и  Точка  имеет координаты  Точка  имеет координату и  Наконец, точка  имеет координаты  а из уравнения  имеем  При значениях  ниже точек  и  но выше вершины параболы у системы два решения. Если  (т. е. на уровне вершины), то решение одно. Также одно решение будет, если  между точками  и  т. е. Таким образом, нужные  - это  и 

Обоснованно получен правильный ответ – 4 балла
С помощью верного рассуждения получен ответ, но в решении допущена вычислительная ошибка или оно недостаточно обосновано – 3 балла
С помощью верного рассуждения получен ответ, но в ходе решения допущена одна ошибка, отличная от вычислительной – 2 балла
Получены некоторые верные значения параметра, однако решение содержит более одной ошибки – 1 балл
Решение не соответствует ни одному из критериев, перечисленных выше – 0 баллов

Ответ: 

Источник: NeoFamily