Равномерное движение по окружности. Закон всемирного тяготения

Динамика дамочка крупная, а как говорится: чем больше, тем сложнее с ней справиться. Но не для нас.

Второй закон Ньютона растет, как только появляется помимо прямолинейного движения, движение по окружности. Хотя суть сильно не меняется.

Напоминаю: второй закон говорит, что равнодействующая сил, действующих на тело, при равноускоренном движении в инерциальной системе отсчета равна произведению массы на ускорение. Или проще, сумма проекций сил, действующих на тело равна массе на ускорение.

А при движении по окружности, у тела всегда есть ускорение, помнишь, мы его центростремительным когда-то называли. Значит при этом, даже если скорость постоянна, всегда будет применяться второй закон Ньютона и результирующая сила (на выбранную ось) будет равна масса на центростремительное ускорение.

Для примера возьмем стандартную задачу на движение автомобиля в повороте:

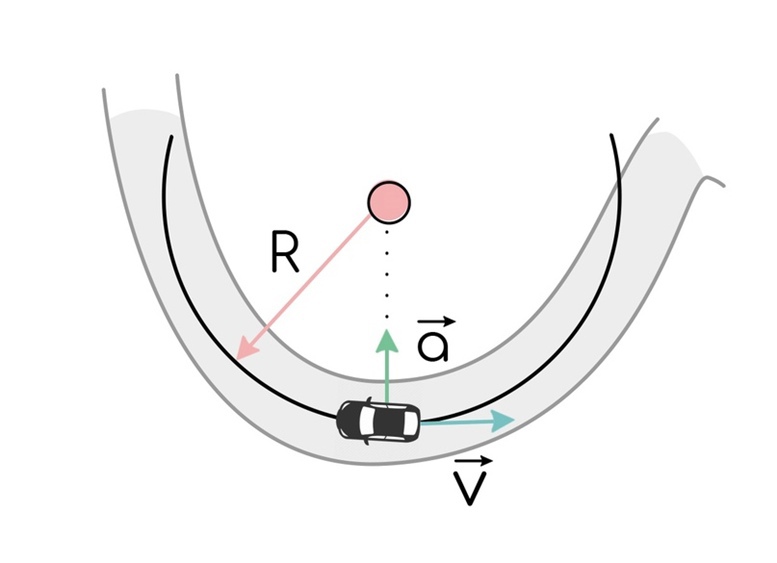
Задавался вопросом: почему автомобиль не улетает с дороги? А если ехать быстро, то все-таки улетает. Конечно, ответ находится в шинах – сцепление с дорогой. Вернее трение. Единственная сила, которая не дает машине съехать – сила трения. Значит она и будет равна равнодействующей ma:

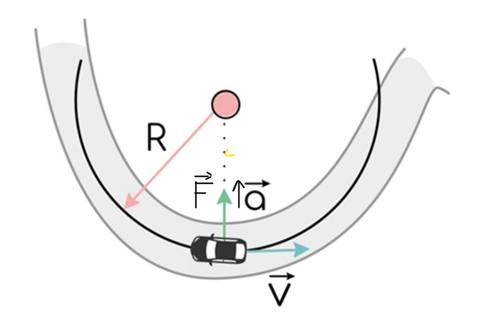
Второй закон Ньютона и в России второй закон, поэтому сумма сил равна ma, а так как сила одна:

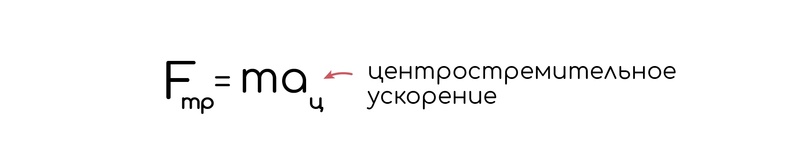
Обычно в задачах просят найти предельно допустимую скорость, с которой возможно движение на повороте определенного радиуса. Конечно это зависит от коэффициента трения тоже и находится все путем расписывания центростремительного ускорения по старой доброй формуле из статьи на движение по окружности:

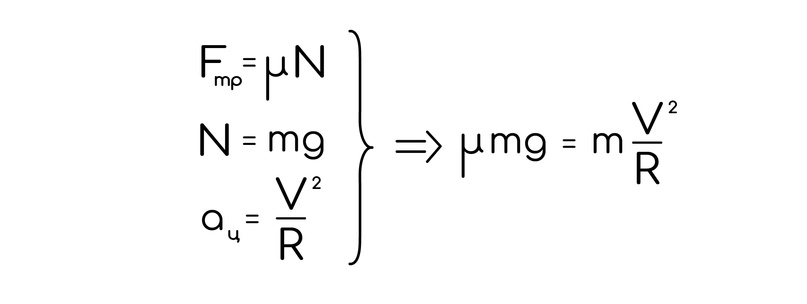
И со спокойной душой находи скорость.

Есть еще одна интересная ситуация, особенно любят это представители капиталистического общества: автомобиль едет по выпуклому и вогнутому мосту и надо узнать в каком из случаев сила давления машины на поверхность больше и на сколько. А для этого надо расставить все силы:

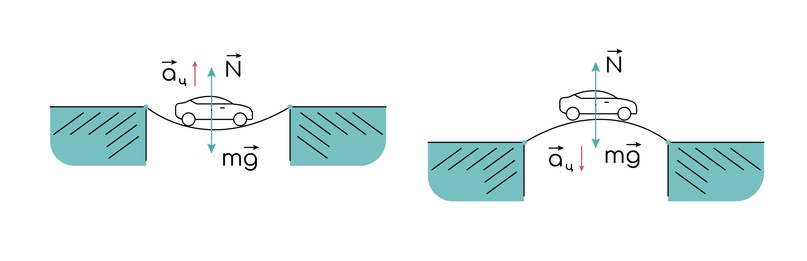
Как видишь ускорение оправдывает название, центростремительное всегда к центру, поэтому имеет разное направление, из-за этого и уравнение сил будут выглядеть по-разному:

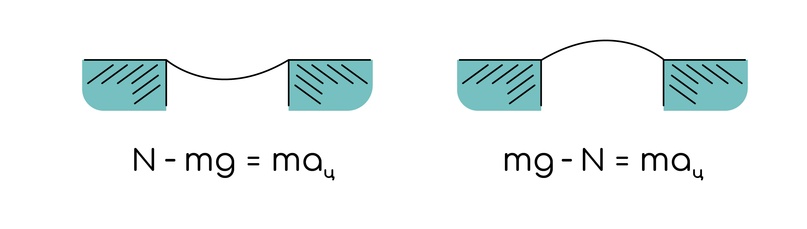
Закон всемирного тяготения

Закон, который, в прямом смысле, держит всю вселенную. Все тела притягиваются друг к другу силами гравитационного взаимодействия. Правда эти силы зависят от массы, поэтому чтобы их почувствовать, тело должно быть размером хотя бы со скалу, или крупный астероид. А находится эта сила по формуле:

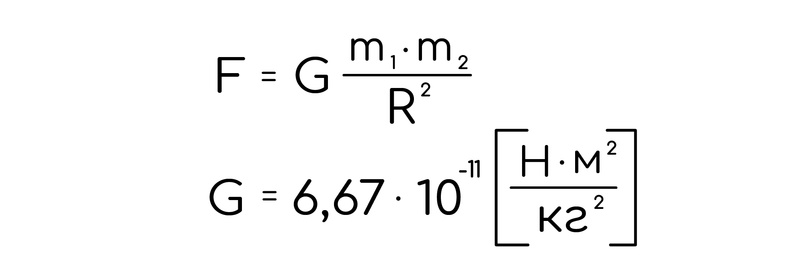
Где m1 и m2 – масса одного и другого тела (планет, или планеты и тела); G – гравитационная постоянная, в справочнике дается; R – расстояние между ЦЕНТРАМИ тел.

Естественно также в совокупности с этим применяются законы Ньютона. Например если вокруг земли летает ракета на расстоянии H:

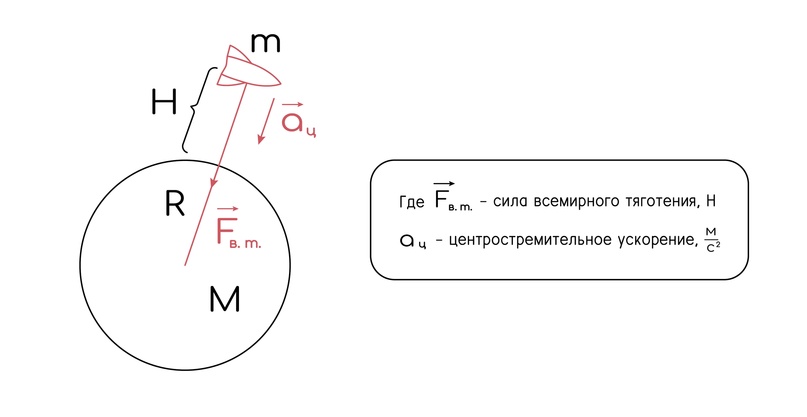
По второму закону Ньютона сила тяготения будет равна массе на ускорение и при расписании получаем:

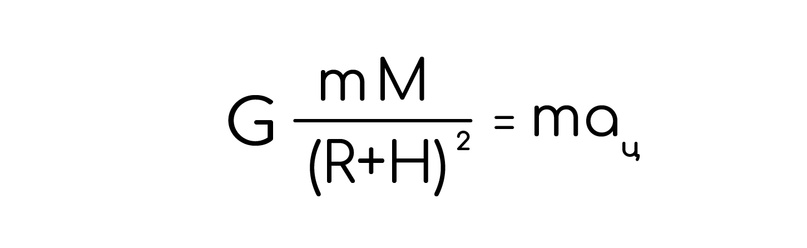
Не забывай про расстояние между центрами. Но есть проблема. Никто тебе не даст массу земли. И как ее найти тогда? Просто: необходимо рассмотреть тело на земле, ведь на земле мы точно знаем g, а сила тяготения на земле как раз будет равна силе тяжести:

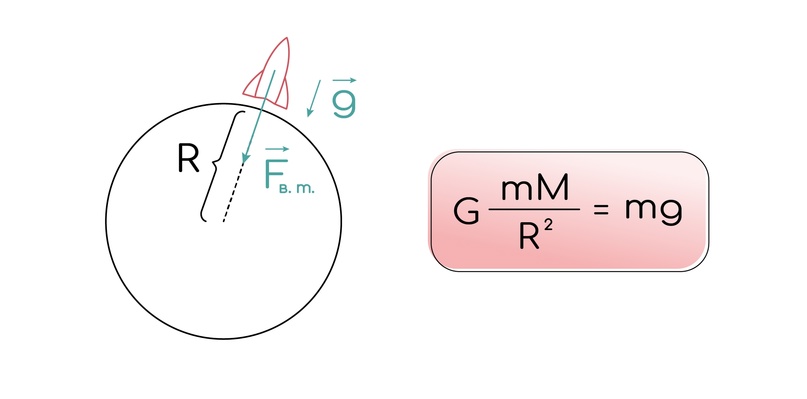
Найдя из этого выражения массу земли M, подставим ее в наш закон Ньютона и будем наслаждаться самой решенной задачей на свете =)