Равномерное движение по окружности

Признайся, ты этого ждал? Или это я ждал? Не суть, короче: равномерное движение по окружности последняя полноценная часть нашей кинематики. Равноускоренное движение — это круто, но оставь это универу, в школе этим только трудовик пугать может.

В движении по окружности есть специфичные величины, а есть такие, с которыми ты уже знаком. С них и начнем.

Скорость

Скорость – это путь, деленный на время. На окружности так же. Только путь будет находиться как длина окружности. Или несколько окружностей (N штук). Ты же помнишь, как найти длину окружности? Тогда скорость найдется:

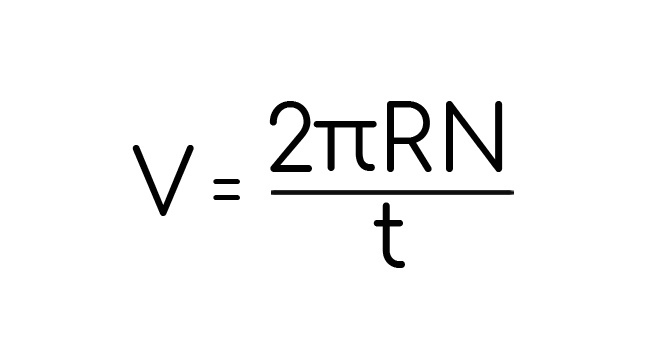
А если сделать универсально: прохождение только одной окружности. Тогда нам не понадобится количество оборотов N, и самое интересное, время одного оборота уже будет называться период, обозначается T. Тогда скорость находится:

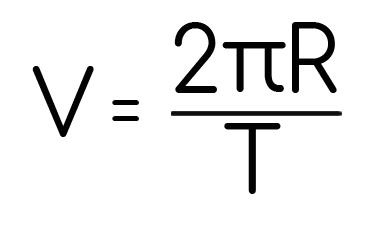
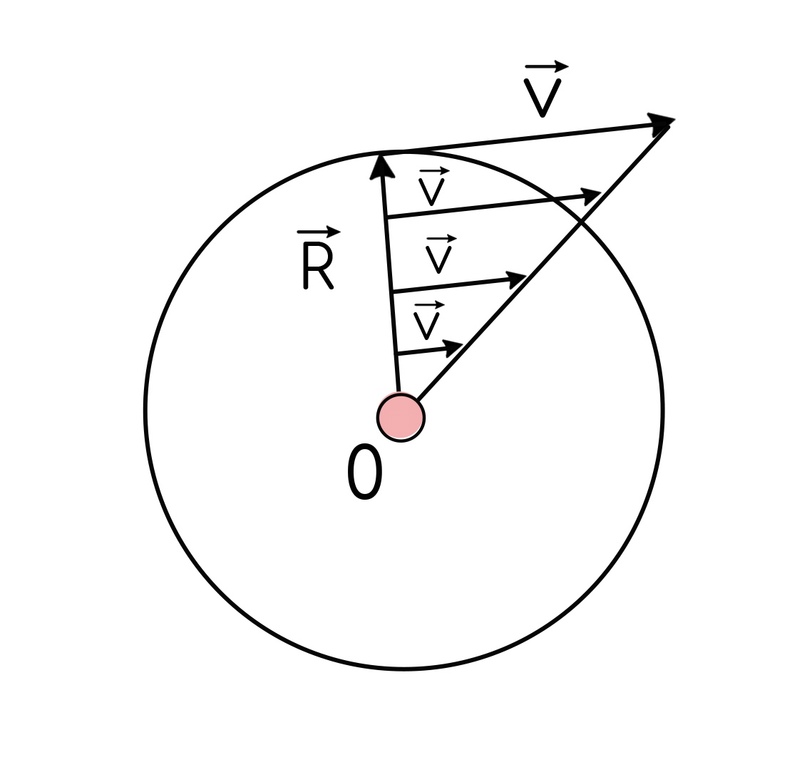
И называется эта скорость линейной, направлена всегда по касательной к окружности:

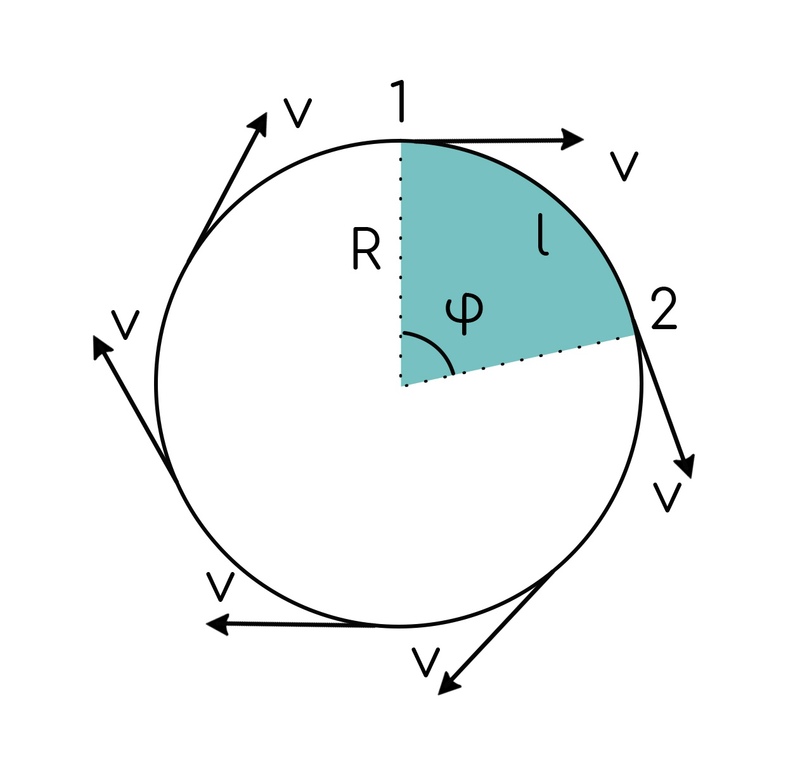
Когда ты раскручиваешь на веревке камень, чтобы отправить быстрое сообщение прямо получателю, он (камень) не летит по кругу. Он летит ровно по линии, продолжая движение в сторону, где ты его отпустил. Это и есть линейная скорость.

Логично предположить, что есть какая-то круговая скорость? Да, ты прав, скоро мы до нее дойдем.

Период

А сейчас еще раз про период: это время одного полного оборота. А если оборотов несколько, N, то можно найти его, если разделить время (t) этих оборотов, на их количество:

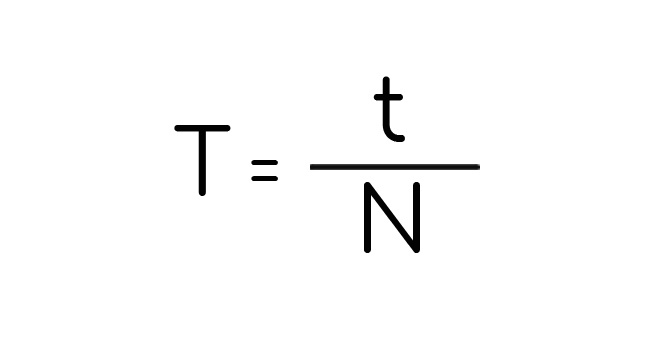
Не забывай про систему СИ: все в метрах и секундах.

Частота

Наверняка слышал про такое понятие, как частота. Частота вращения, количество оборотов в секунду, минуту. Очень распространенная характеристика, мы ее обозначим буквой «ню» и найдем как количество оборотов, за время вращения, измеряется 1/с:

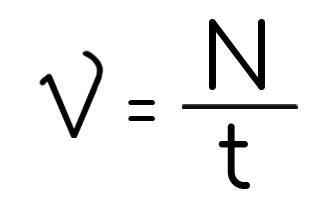
Как период, только перевернуто.

Да, действительно, можно и так выразить:

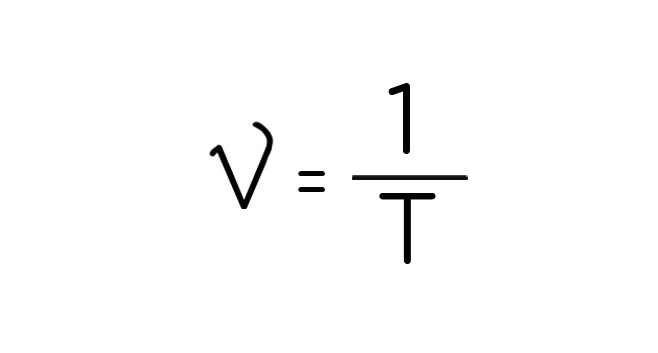
Угловая скорость

Еще одна специфичная для окружности величина – угловая скорость (в колебательном движении ее называют еще циклической частотой) обозначается буквой «омега», находится по аналогии с линейной скорости, только путь теперь угол:

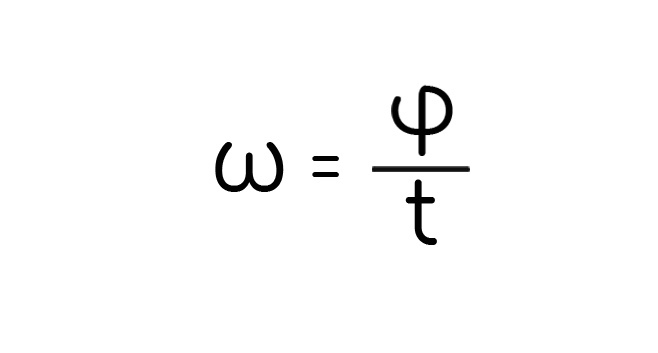
Измеряется тоже 1/с. Если снова универсализировать, крутое слово, взять один оборот, который равен, кажется, 360 градусов, или 2pi, а время тогда равно периоду:

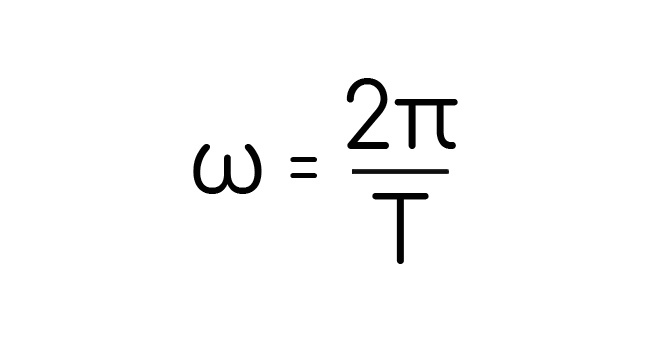
Посмотри на линейную скорость, там тоже есть два пи делить на период, может заменим на омегу? Тогда выйдет такая штука:

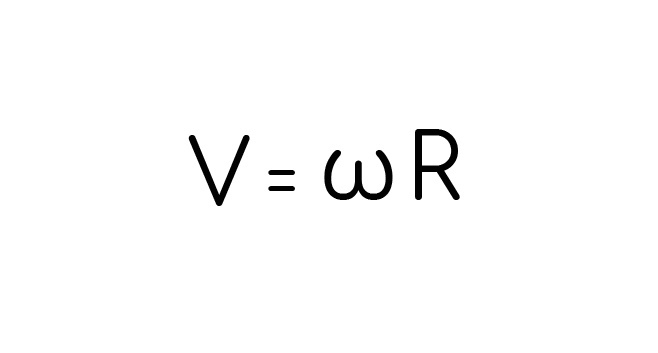
Но это выводы, в конце я приведу еще парочку.

А пока поговорим про еще одну очень важную вещь, которая есть только при движении по окружности: центростремительное ускорение.

Стой стой стой. Движение же равномерное, какое ускорение?

Центростремительное ускорение

Дело в том, что при любом отклонении от прямолинейного движения появляется ускорение. Представь, как ты едешь в своем дорогом мерседес-бенз майбах на физру. Что ты чувствуешь, когда твой водитель даже немного поворачивает? Тебя отклоняет в сторону.

Тоже самое чувствуют обычные люди в автобусе или метро, при повороте они теряют равновесие. Происходит это из-за действия очень сложной вещи, называемой инерцией. Оставим ее определение тоже университету. А еще лучше чувствуется это, когда ты находишься на любой вращающейся карусели.

Вот эти все ощущения, что на тебя что-то действует, следствия ускорения, которое есть всегда, при движении по окружности. Оно называется центростремительным.

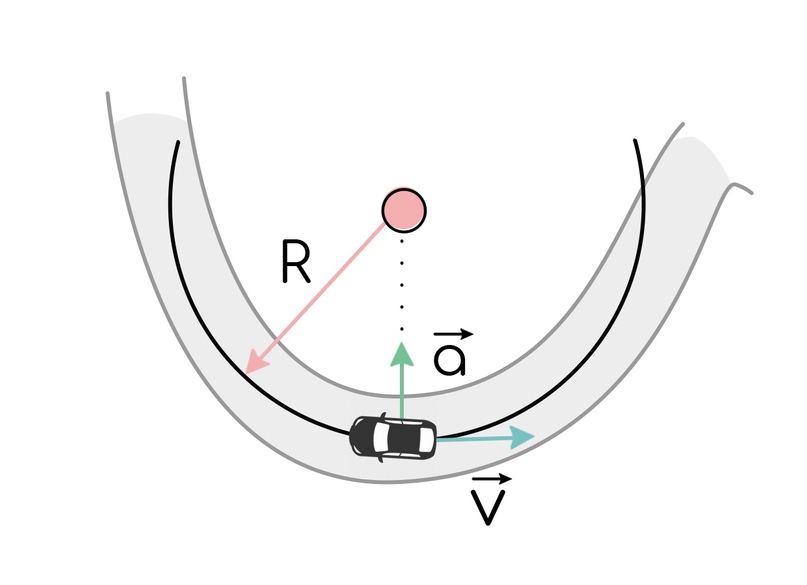
Парадокс: с карусельки выкидывает тебя наружу, а называется ускорение центростремительным. И на рисунках оно направляется к центру. Это тоже все связано с инерцией, а нам лучше считать, что это сделано для удобства. Когда в динамике мы с этим встретимся, увидишь, что это действительно удобно.

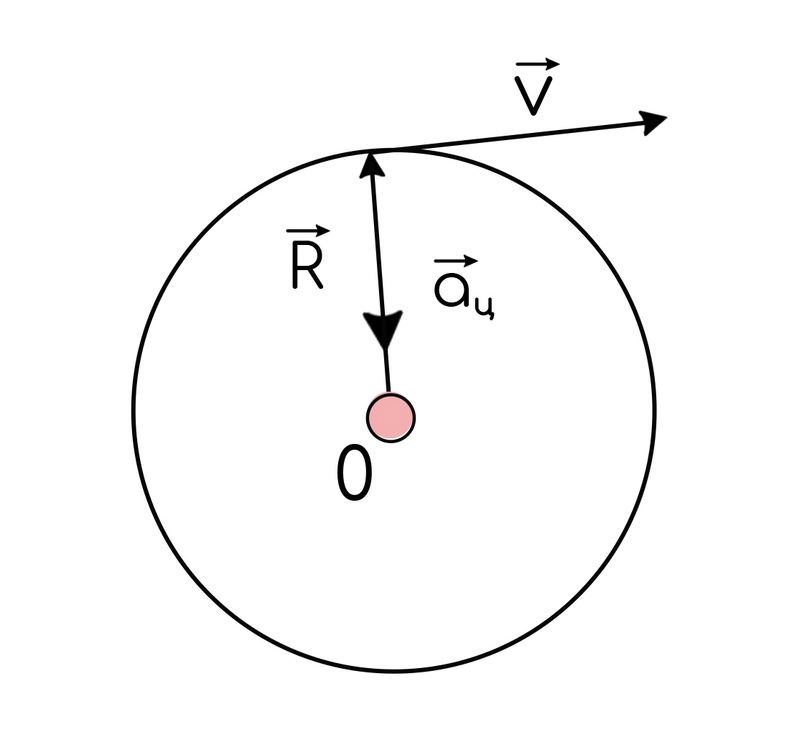
Основная формула для нахождения этого ускорения:

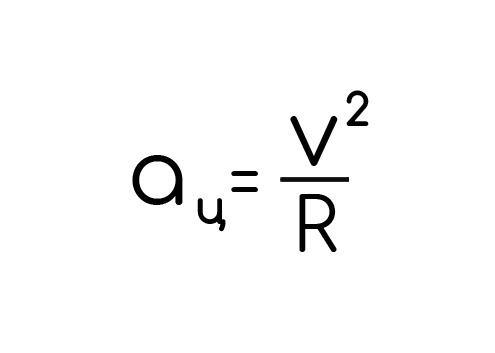
Важная вещь: внимательно посмотри на формулы, в некоторых есть радиус, в некоторых нет. Это значит величины, вроде частоты, периода, угловой скорости, которые специфичны для окружности, постоянны в любой точке этой окружности (мы не на русском, тавтология — это святое). А линейная скорость и центростремительное ускорение зависят от радиуса, а значит в разных точках они отличаются. Чем дальше от центра, тем больше будут эти величины.

Зависят они при удалении от центра примерно так:

Еще пара формул, на всякий случай, которые можно вывести, для центростремительного ускорения, чтобы ты был максимально вооружен.

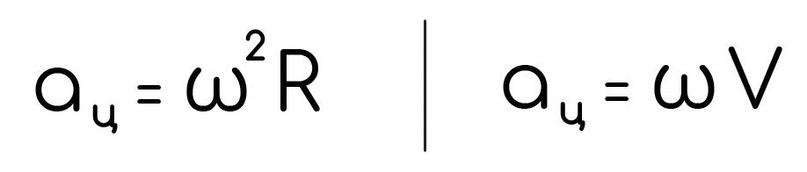
Отдельного рассмотрения требует тема редукторов, ременных передач и других соединений нескольких окружностей. Но это уже совсем другая история. До встречи, в следующей статье =)