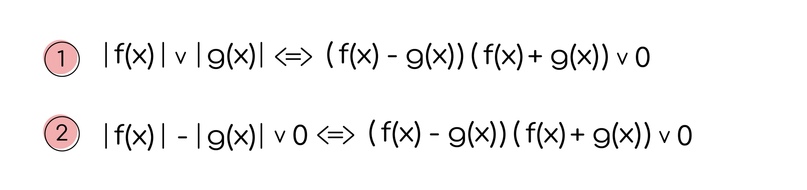Равносильные переходы с модулями и корнями

***

В предыдущей статье мы говорили о равносильных переходах для логарифмов и степеней. В этой статье обсудим преобразования, которые позволяют упрощать неравенства с модулями и корнями.

1) Сравнение модуля с числом

Идея в том, что в случае, когда сравниваются неотрицательные выражения, мы можем оба таких неотрицательных выражения возвести в квадрат. Мы это делаем для того, чтобы избавиться от модуля.

Если модуль возведен в квадрат, то модуль можно убрать.

Если же мы наблюдаем разность неотрицательных выражений, то преобразование немного другое. В этом случае нам необходимо домножить обе части неравенства на сопряженное, чтобы получить разность квадратов, которая уберет модуль.

Обращаю ваше внимание на то, что в этом случае мы домножим на выражение, которое будет положительным (несмотря на то, что оно с переменной), а значит знак неравенства не поменяется.

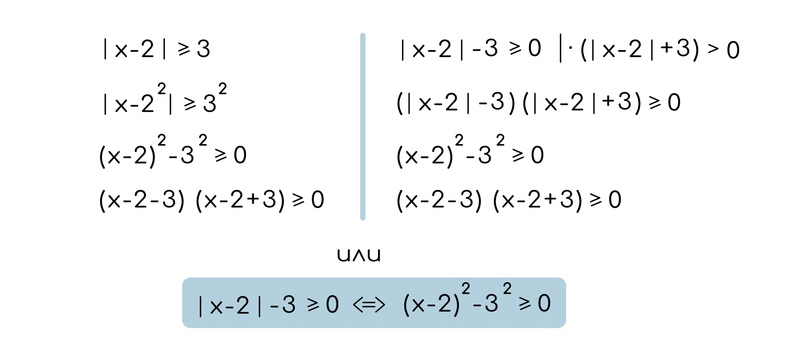
2) Сравнение модулей

Идеи все те же. За счет того, что мы можем утверждать, что модуль является неотрицательным числом, можно возводить в квадрат обе части неравенства в квадрат или домножать на сопряженное.

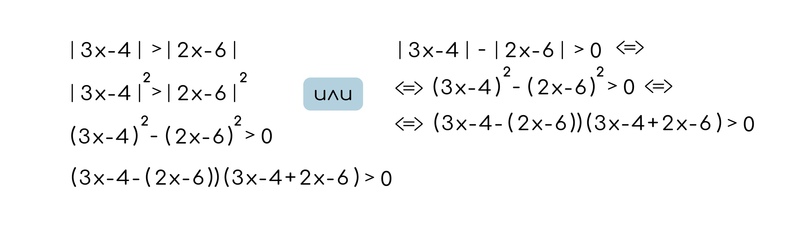
В правом случае мы не возводим в квадрат обе части, а применяем равносильный переход.

3) Переходы с корнями

Как и в предыдущих случаях, мы говорим о том, что сам по себе корень является неотрицательным числом, а значит можно выполнить следующий переход в неравенстве:

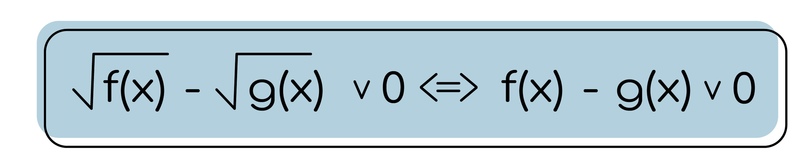
Тут мы тоже можем домножить на сопряженное, чтобы убрать корни.

Комбинированные случаи

Стоит отметить, что все эти переходы работают для любых множителей, которые будут сравниваться с 0 (для этого необходимо, чтобы вся левая часть была разложена на множители):

***
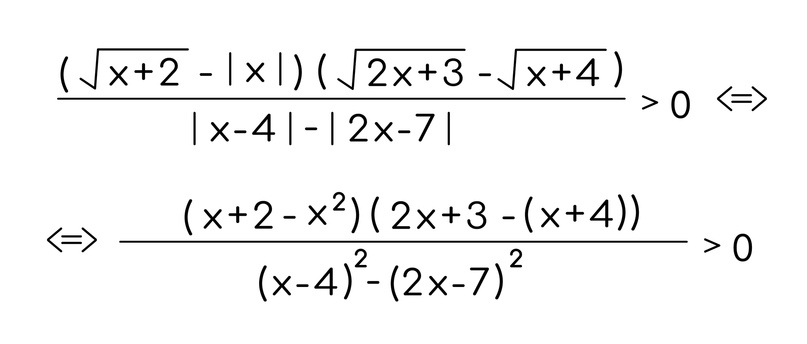