Формулы для показательных выражений и уравнений

***

Показательные выражения и уравнения встречаются как в первой, так и во второй части экзамена в различных форматах.

Формулы, которые вам нужно знать, не очень сложные, но запомнить их все равно необходимо. А еще лучше понять, как и почему они так работают.

Для начала давайте вспомним, как появилась запись степени.

***

Смысл степени

Представим, что мы 2 умножаем само на себя 5 раз. В таком случае говорят, что у нас будет 2⁵.

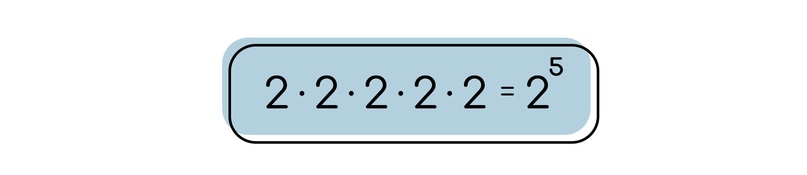
Сложение и вычитание степеней

Если мы перемножаем одинаковые основания, то степени складываются.

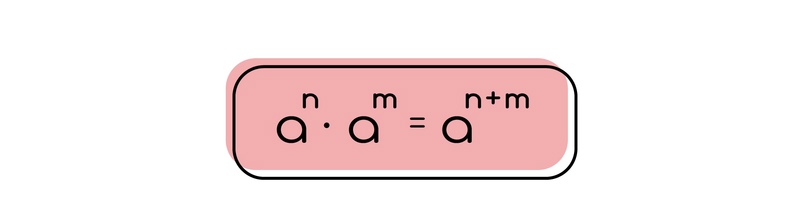
Для примера давайте умножим 2² и 2¹, можно расписать их как 2 умноженное на 2 и просто 2, тогда при перемножении мы можем сказать, что получится 2³ по смыслу степени.

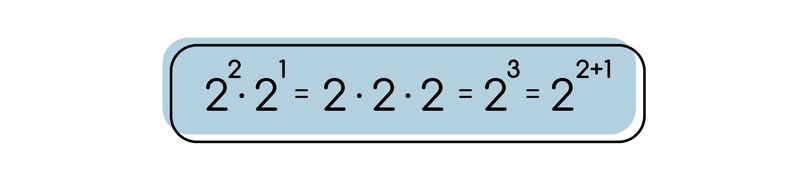
При делении степени будут вычитаться.

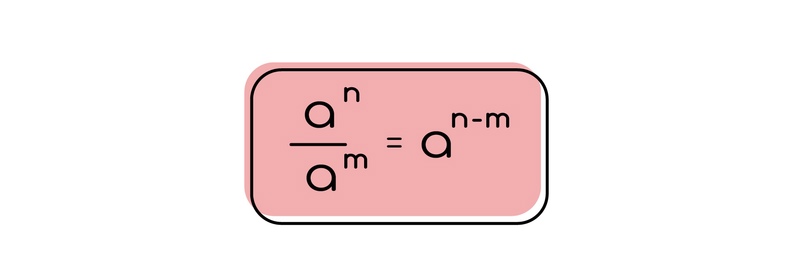
Число в нулевой степени

Теперь давайте разберемся с тем, что по смыслу означает число в нулевой степени.

Начнем с другого. Давайте вспомним, что будет, если мы какое-то число поделим само на себя? Это отношение будет равно единице. Но теперь воспользуемся формулой выше и скажем, что если мы число делим само на себя, то это все равно что сказать, что основание оставляем то же, а из степени 1 мы вычитаем степень 1, и 1 — 1 = 0. То есть мы можем сказать, что число в 0 степени — это число, деленное само на себя.

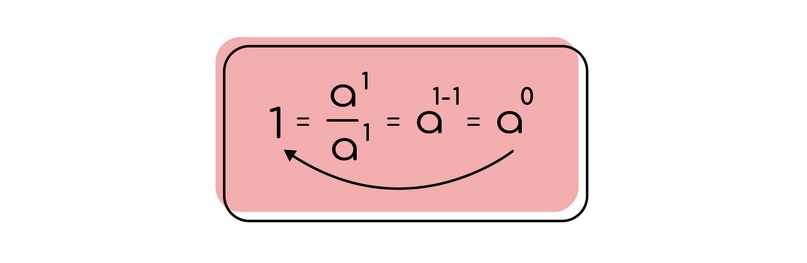
Число в отрицательной степени

Дальше разберемся в том, как можно объяснить отрицательную степень.

Допустим есть число в степени -n, ее можно представить как 0 — n (это же никто не запрещает). Тогда разложим разность степеней через деление. Как мы уже знаем, число в 0 степени равно 1, тогда остается следующее выражение:

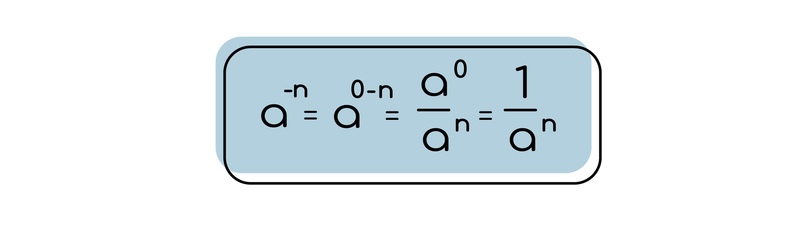
Степень в степени

Как понять, почему при возведении числа в некоторой степени в еще какую-то степень, степени перемножаются?

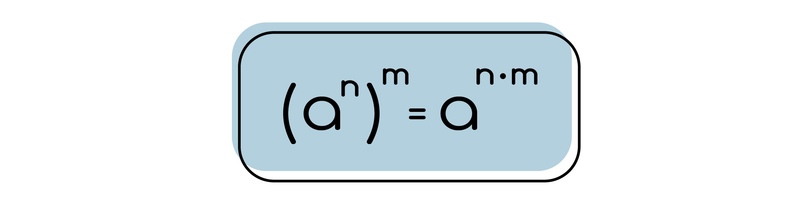
Снова вернемся к смыслу того, откуда берется степень.

Представим 2³, которое еще возведено во 2 степень. Тогда мы можем сказать, что это все равно что 2³ умножить на еще одно 2³. Но при перемножении одинаковых оснований степени складываются. Значит получится в степени 3+3, или по-другому 3 умноженное на 2.

Дробная степень

Осталось еще вспомнить, как правильно воспринимать дробную степень.

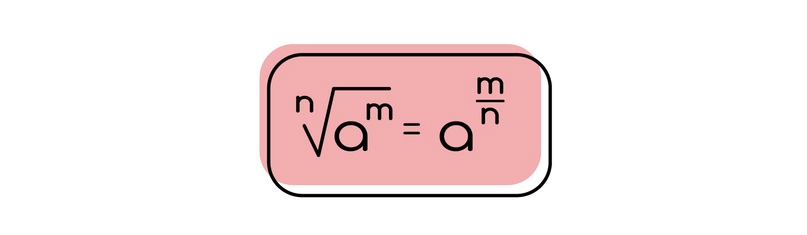
Здесь лучше снова все понять на конкретном примере.

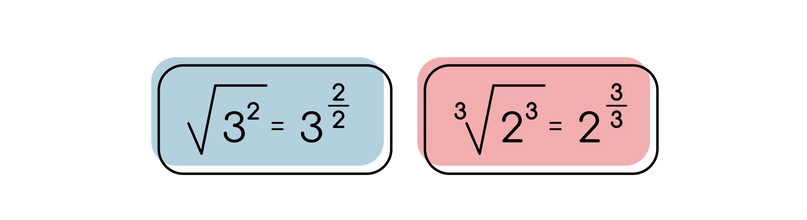
Допустим у нас есть число 9. Мы можем сказать, что это 3². Как теперь избавиться от этой двойки, чтобы получилось число 3? Для этого необходимо либо извлечь квадратный корень, либо поделить эту степень на 2, чтобы получить 3¹.

Если у нас есть 8, то можно сказать, что это 2³ степени. Как тут избавиться от куба? Снова мы либо извлекаем корень третьей степени, либо делим степень на 3, чтобы получить 2¹.

То есть когда мы делим степень на какое-то число, то мы извлекаем корень этой степени из числа.

Произведения и дроби в степенях

Также стоит вспомнить, что если мы произведение/дробь возводим в какую-то степень, то мы каждый множитель/(числитель и знаменатель) возводим в эту степень.

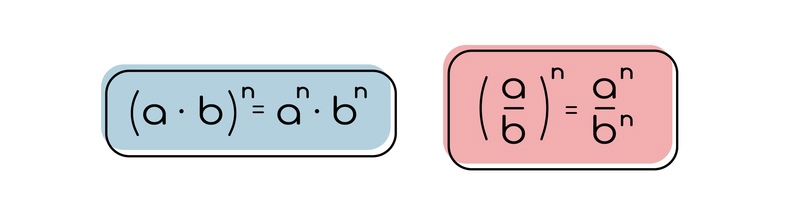
Но это работает в обе стороны, поэтому если у вас есть умножение/деление разных оснований, которые находятся в одинаковых степенях, то эту степень можно вынести.

***