Свойства чисел

В этой статье мы разберем все, что тебе нужно знать для успешного решения заданий №19 в базовой математике.

В основном речь пойдет о делимости чисел. Разберемся в том, как это работает, откуда берется и как получать делимость на другие числа, опираясь на базовые знания о тех, которые мы подробно тут разберем :)

Приятного изучения!

Основные признаки делимости

Делимость на 2

Тут все просто. Число делится на 2, если оно оканчивается на цифру, которая делится на 2.

Можно просто сказать, что число должно быть четным, но дальше вы увидите, почему я написал это именно в таком формате.

Пример:

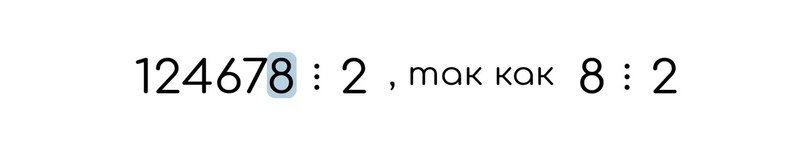
Делимость на 4

Мы еще вернемся к делимости на 3, но сейчас разберем все делимости, связанные с двойкой.

Число делится на 4, если последние две цифры исходного числа образуют значение, которое делится на 4.

Почему в игру теперь вступают именно 2 цифры?

Смотрите, любое число можно представить в формате какого-то количества сотен + остаток от деления на 100.

Возьмем число 536. Его можно представить как 5 раз по 100 + 36. Любое выражение, которое содердит в себе множитель 100 автоматом будет делится на 4 (так как 100 делится на 4), поэтому для проверки того, будет ли 536 делится на 4, можно лишь проверить, делится ли 36 на 4.

Ну и так как 36 делится на 4, значит и 536 делится на 4.

Делимость на 8

Тут все аналогично происходит. Только теперь последние 3 цифры числа должны образовать значение, которое делится на 8.

Пример:

Делимость на 16, 32, 64 …

Дальше вы для 16 берете последние 4 цифры, для 32 последние 5 цифр и т.д.

На экзамене дальше 8 крайне редко делимость спрашивается, но все равно лучше понимать, как самостоятельно вспомнить и другие делимости, если что-то подобное попадется.

Делимость на 3

Число делится на 3, если сумма его цифр делится на 3.

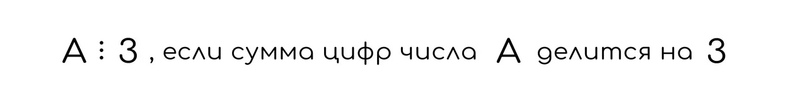
Пример:

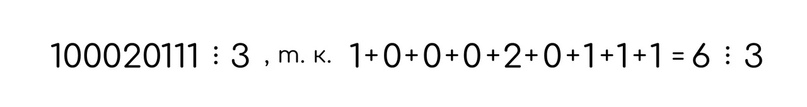
Делимость на 9

Число делится на 9, если сумма цифр делится на 9.

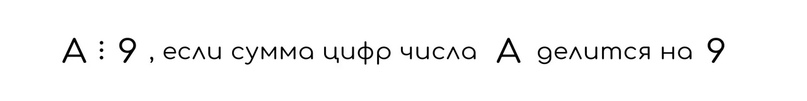
Пример:

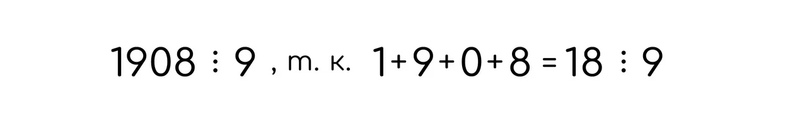
Делимость на 11

Это, пожалуй, самая интересная делимость из всех, которые вам нужно знать для экзамена.

Число делится на 11, если суммы чисел на четных позициях и нечетных позициях равны, или модуль разности таких сумм делится на 11.

Звучит запутанно, но на конкретных примерах все будет сильно понятнее. Уточню, что под четными и нечетными позициями подразумеваются разряды, а не сами четные или нечетные цифры числа.

Пример:

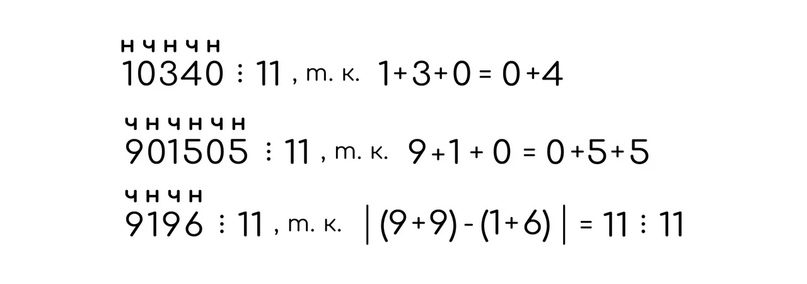
Делимость на 5 и на 10

Число делится на 5, если оно оканчивается на 0 или 5.

Число делится на 10, если оно оканчивается на 0.

Тут все максимально просто, обойдемся без примера)

Сразу скажу, что делимость на 7 вам в заданиях не встретится, поэтому разбирать ее не будем (признак там не очень приятный, но для общего сведения можете его посмотреть)

Теперь будем переходить к понимаю более сложных комбинированных делимостей, которые вы можете встретить на экзамене.

***

Комбинирование делимости

Для того, чтобы понять необходимые условия для делимости на другие значения, необходимо эти значения разбить на множители (желательно на те, что представлены выше в первой части статьи) и объединить условия каждого такого множителя.

Начнем сразу с примеров. Допустим, мы хотим понять условие для делимости на 55. Разложим 55 на произведение 5 и 11. Тогда, чтобы число делилось на 55, оно должно делиться на 5 и на 11. Эти признаки мы уже знаем.

Пусть есть вот такое число 135245. Проверим, делится ли оно на 55:

Сейчас будет более хитрый пример.

Давайте попробуем сформулировать признак делимости на 24.

Можно разложить 24 на 6 и 4, а можно на 8 и 3. Какое же выбрать?

Лучше выбирать те множители, которые имеют некомбинированный признак.

Делимость на 6 будет содержать в себе делимость на 2 и на 3, поэтому лучше сразу ставить условие, что число делится на 24, если делится на 8 и на 3.

Таким образом вы сможете выявлять любые другие делимости, которые встретятся вам в заданиях экзамена.

Пример задачи экзамена

Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.

Что мы видим?) Делимость на 24. Значит число должно делится на 8 и на 3.

Для этого сумма его цифр должна делится на 3 и последние 3 цифры должны делится на 8.

Раз у нас число может состоять только из 0 и 1, то делимость на 8 может быть организована постановкой трех нулей вместо последних трех цифр.

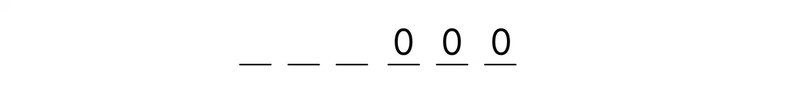
Ну а теперь подумаем, какие должны быть первые три цифры, чтобы сумма всех шести делилась на 3?

Только если мы поставим все три единицы)

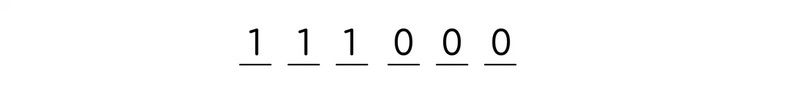
Поздравляю! Мы решили задание и привели конкретный пример числа!