- Умный справочник
- Математика (база)
- Производная в базовой математике
Производная в базовой математике
В этой статье мы разберем все, что тебе нужно знать про производную для решения 14-ого номера базовой математики)
Поехали!
Общие сведения о производной
Определение и общие сведения
Есть множество определений, которые дают в различных учебниках, однако для экзамена достаточно запомнить одно:
Производная показывает как и с какой скоростью изменяется функция.
Обозначается черточкой.
Теперь поговорим о знаках производной:
- Если график функции растет — производная больше 0 (положительное изменение)
- Если график падает — производная меньше 0 (отрицательное изменение)
- Если значения функции не меняются — производная равна 0 (нулевое изменение)
Точки, в которых происходят смены знака производной — точки экстремума.
Сами значения функции в точках экстремума называются просто экстремумами.
Точка экстремума — координата х.
Экстремум — координата y.
Схематично отобразим описанное выше:
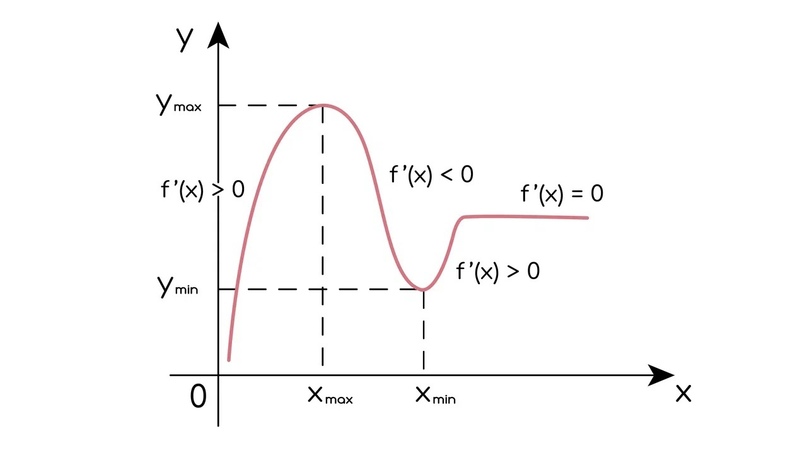
Геометрический смысл производной
Для того, чтобы найти производную в какой-то точке графика функции, вам необходимо построить касательную в эту точку графика функции.
В таком случае справедливы следующие факты:
- В точке касания значения функции и касательной равны
- В точке касания производные функции и касательной равны (у прямых в любых точках производные одинаковые)
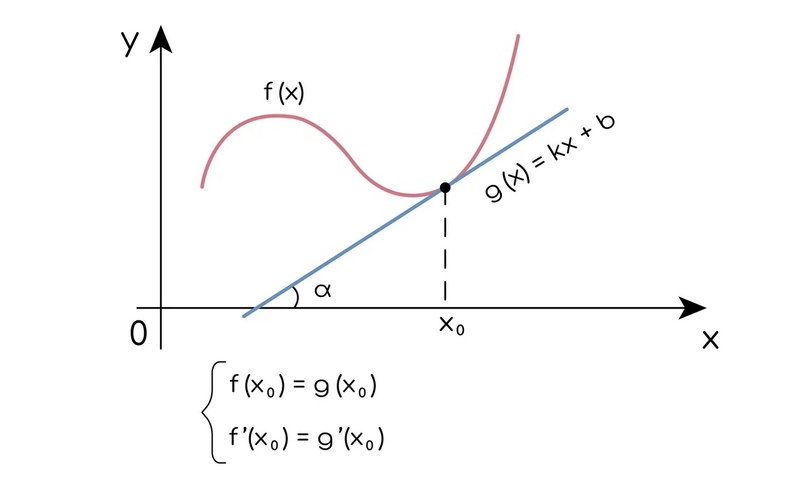
Для заданий базы вам важно запомнить то, что производная в точке касания равна коэффициенту k у касательной (вообще k еще можно найти как тангенс угла наклона, но вам в базе такие задания не встретятся)
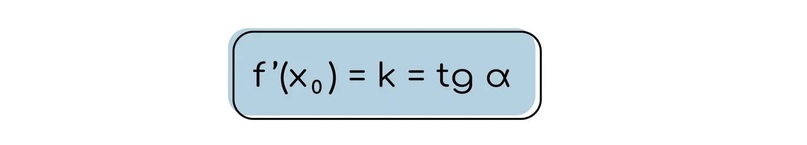
Как же это использовать в заданиях?
1) Смотрим на касательные
2) Если она растет, то производная в точке положительная, если падает, то отрицательная
3) Там, где касательная растет быстрее, более положительная производная
4) Там, где касательная падает быстрее, более отрицательная производная
Рассмотрим вот такое задание из базы:
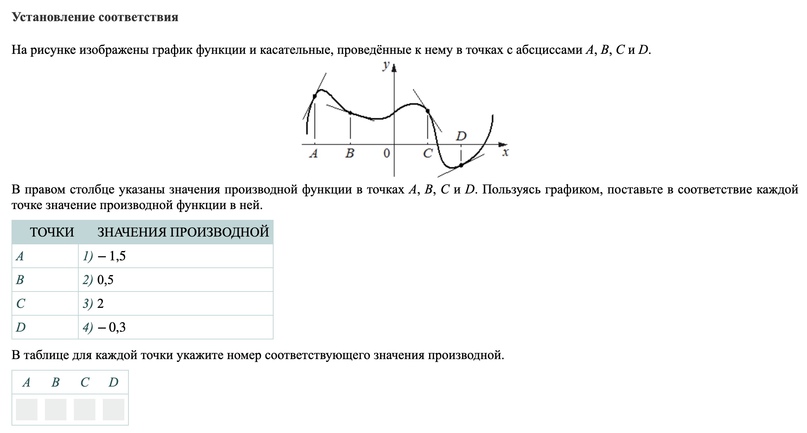
Посмотрим, в каких точках касательные растут. Это А и D.
Где они убывают? В B и C.
Где растет быстрее? В точке А, значит там выбираем ответ номер 3. Для D ответ номер 2.
Где убывает быстрее? В точке С. Значит в ней выбираем ответ 1. Для В выбираем оставшийся ответ под номером 4.
