Графики функций

Умение работать с функциями пригодится во многих заданиях экзамена. В первой части этому посвящен отдельный номер.

Будем разбирать основные функции, которые чаще всего встречаются в заданиях базовой математики.

Начнем с рассмотрения линейной функции.

Линейная функция

Общий вид

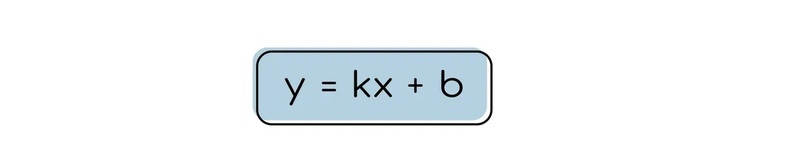
X и Y в этом уравнении — координаты точек, которые лежат на прямой.

Рассмотрим линейную функцию y=2x+1.

Точка с координатами (0;1) превращает данное уравнение в верное равенство (1=2*0+1), поэтому прямая проходит через эту точку.

Точка с координатами (5;3) не превращает данное уравнение в верное равенство, а значит прямая не проходит через данную точку.

Работа с коэффициентами

Коэффициент b отвечает за пересечение с осью Oу.

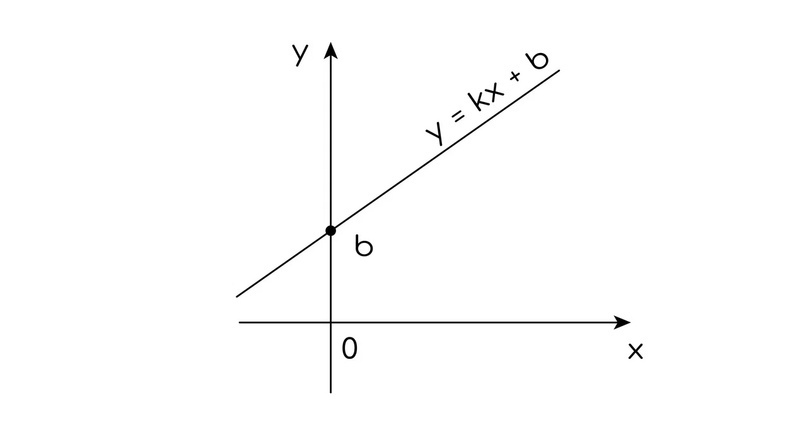
Если мы вместо x подставим значение 0, то получим, что y=k*0+b, то есть y=b.

Коэффициент k (угловой коэффициент) отвечает за «направление прямой» и за ее скорость роста/падения.

Если k>0, то прямая растет. При этом чем больше по модулю k, тем быстрее растет прямая (ближе к оси Oy).

Если k<0, то прямая убывает. При этом чем больше по модулю k, тем быстрее убывает прямая.

Также угловой коэффициент можно найти с помощью тангенса угла наклона.

Разберем все на конкретном примере:

Нарисуем прямую y=2x+1 и отметим угол наклона прямой к оси Ox.

Теперь рассмотрим прямоугольный треугольник с углом альфа и найдем тангенс этого угла в данном треугольнике.

В случаях, когда вам необходимо будет найти общий вид по точкам, вы можете найти k через тангенс угла наклона, что поможет вам быстрее решить задание.

Немного другие виды прямых

Горизонтальная прямая имеет вид y=a.

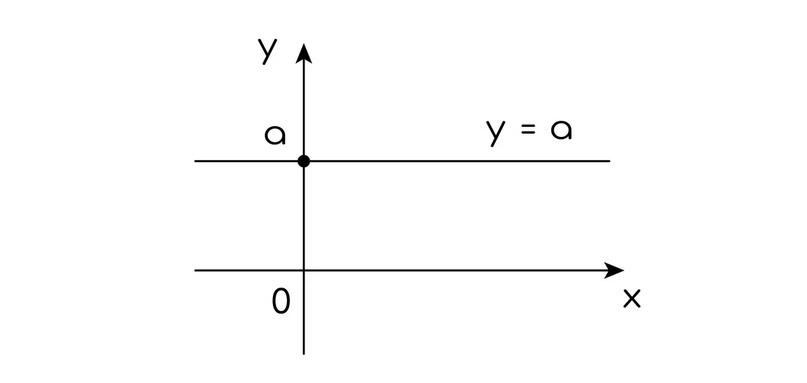
Это прямая, у которой k=0, поэтому значения x никак не влияют на значения y.

Вертикальная прямая имеет вид х=а.

Здесь исчезает y. Но как? Мы же не можем получить коэффициент 0 перед y?

На самом деле можем. Дело в том, что уравнение прямой можно записать вот в таком формате:

Если здесь выразить y через x, то мы получим общий вид, с которым мы работали до этого.

Как раз в этом виде мы и замечаем коэффициент перед y, который может равняться 0.

***

Квадратичная функция

Общий вид

Общий вид квадратичной функции следующий:

Графиком данной функции является парабола.

Работа с коэффициентами

Коэффициент а отвечает за направление ветвей параболы. Коэффициент с — за пересечение с осью Оу. Коэффициент b — за смещение вправо/влево. Находят его по формуле координаты вершины параболы.