Совместное движение

В предыдущей статье мы говорили о движении по воде. Во многих таких заданиях появляется совместное движение, где объекты движутся либо навстречу друг другу, либо в одном направлении.

В этой статье как раз подробно рассмотрим такие прототипы заданий.

Движение в противоположных направляениях

Начнем с движения в противоположных направлениях. Обычно в этих заданиях объекты движутся именно навстречу друг другу, но в теории это будет работать и когда объекты будут отдаляться друг от друга.

Рассмотрим такую модель и поймем, что поменяется в работе с используемыми формулами.

Для начала представим себе ситуацию, когда два объекта движутся навстречу друг другу. Между ними есть какое-то расстояние. Мы понимаем, что в какой-то момент они встретятся. Давайте рассмотрим именно этот момент встречи:

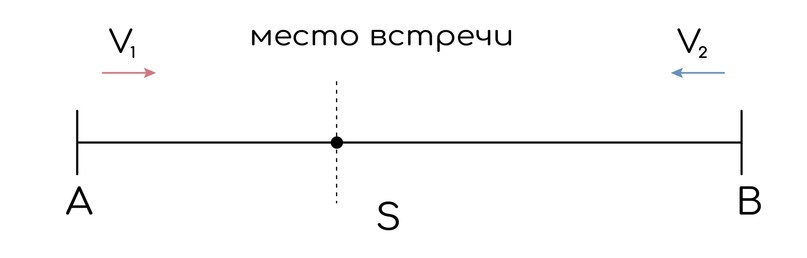
К моменту, когда объекты встретятся, каждый из них пройдет какое-то расстояние, и эти расстояния в сумме будут равны общему расстоянию между объектами, которое было в момент начала их совместного движения:

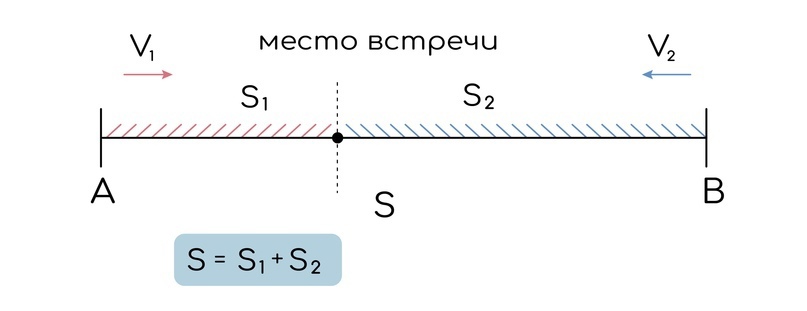
Теперь распишем путь первого и второго. При рассмотрении совместного движения в момент встречи они потратят одинаковое время на дорогу до этого самого места встречи:

Так мы получаем формулу, которую мы можем использовать при рассмотрении движения навстречу другу другу. Теперь давайте рассмотрим несколько прототипов заданий:

Первый прототип

Для начала поймем, что из условия задачи следует, что автомобили двигались совместно не все время. Первый час первый автомобиль двигался 1. За этот час он успеет проехать 60 км, и только после этого начнется совместное движение. При этом, расстояние между объектами будет уже не 435 км, а 375 км:

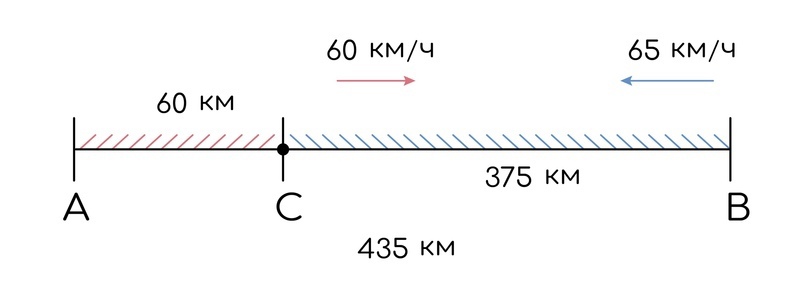
Теперь мы можем рассмотреть совместное движение. Раз они где-то встретятся, мы можем по имеющейся информации найти время, через которое они встретятся:

Нас спрашивают, на каком расстоянии от А автомобили встретятся. Мы можем найти это как расстояние, которое прошел первый автомобиль до точки А. Мы знаем его скорость, а также знаем, что до места встречи он ехал 1 час один и еще 3 часа совместно со вторым. То есть всего ехал 4 часа. Тогда:

Рассмотрим еще один интересный прототип

В этой задаче сначала составим таблицу. Путь нам не дали, но и каких-то опорных значений нет, поэтому возьмем 1 вместо пути:

Теперь надо как-то составить уравнение. Для этого используем информацию о том, что велосипедист и мотоциклист встретились через 1,5 часа. То есть мы знаем их время встречи. Тогда мы можем просто известую нам информацию подставить в формулу, которую мы выводили (не забываем, что путь/изначальное расстояние между объектами равно 1):

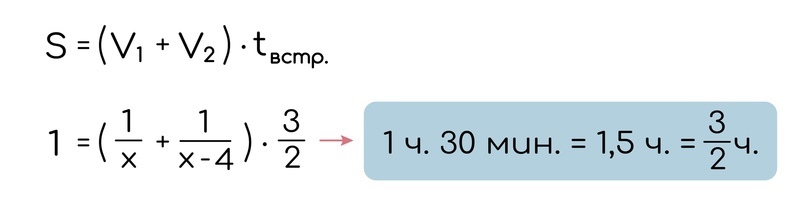
Если теперь все поделить на 1,5, то получим вот такое уравнение:

Это не очень удобное уравнение для подбора, но даже тут есть некоторый способ, который облегчит нам жизнь. Мы же понимаем, что икс как минимум 5 (чтобы время мотоциклиста было не отрицательным). Так давайте попробуем подставить 5:

Не получилось, не фартануло. Но ладно, давайте 6 попробуем тогда:

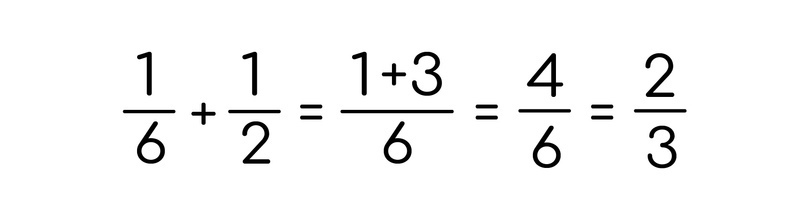
Отлично :)

Все подошло, значит ответ 6. IT JUST WORKS!

Движение в одном направлении

Теперь разберем другой вид совместного движения. Тоже на картинках.

Представим себе ситуацию, когда объекты вышли из одного места в одном направлении и двигались одинаковое время. Очевидно, что если у них разные скорости, то кто-то пройдет больше. А теперь давайте разберемся, как правильно записать это расстояние, на которое один обгонит другого:

По итогу мы можем теперь сказать, что расстояние, на которое один обгоняет другого, на самом деле можно воспринимать как такое расстояние, которое разница скоростей пройдет за какое-то время.

Рассмотрим все на конкретном задании

В этой задаче мы видим, что один обогнал другого на 300м за время, которое нас спрашивают. Тогда мы просто можем сказать, что 300м — такое расстояние, которое прошла разница скоростей за искомое время. И дело в том, что как раз разницу скоростей нам уже дали:

Вообще задачи на движение в одном направлении мы рассмотрим более подробно на движении по окружности, так что это вы увидете в соответствующей статье :)