Задачи на производительность труда

Текстовые задачи в егэ в основном ориентируются на одну формулу, с которой вам предстоит работать.

Это формула, показывающая взаимосвязь между скоростью, временем и расстоянием.

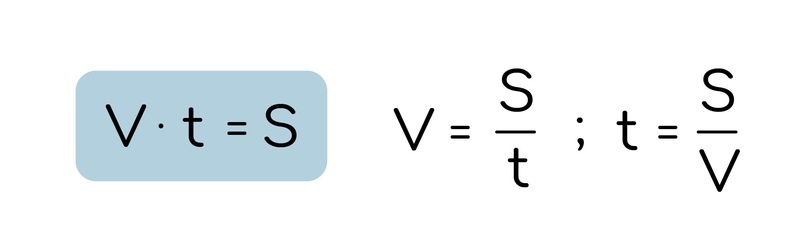
В задачах на производительность труда вместо скорости используют производительность (количество чего-то/единица времени), а вместо расстояния используют работу (количество сделанных деталей и т.д.)

Сложности могут возникнуть при решении конкретных прототипов заданий, где важно разобраться в идее решения.

Как раз о таких различных прототипах мы и поговорим :)

1) Совместный труд

Почти во всех таких заданиях стоит составлять таблицу, где вы в столбиках будете указывать производительность (скорость), время и работу (расстояние), а в строчках будете прописывать рабочих:

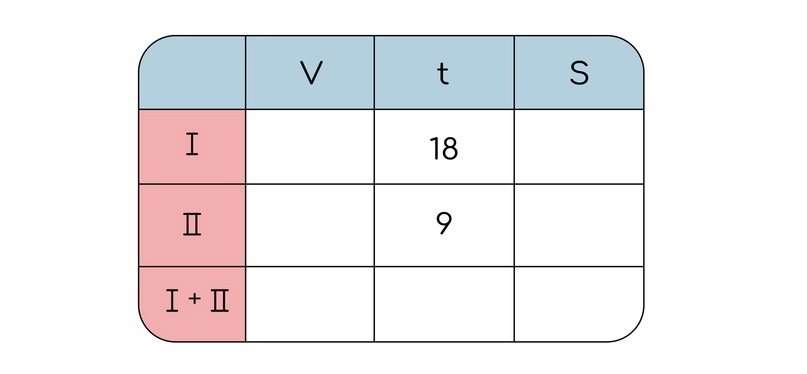
Дальше обращаем внимание на то, что в заданиях, где кто-то начинает работать вместе, вы складываете именно их производительность.

Если первый делает 1 деталь в час, а второй делает 2 детали в час, то вместе они делают 3 детали в час.

Поэтому нам необходимо выразить скорость первого и второго, чтобы потом ее можно было сложить.

Но вот беда. Мы не знаем работы.

Иногда говорят, что в этом случае мы берем за работу 1, но на самом деле все гораздо интереснее.

Давайте сейчас решим все максимально честно и введем переменную, вместо работы.

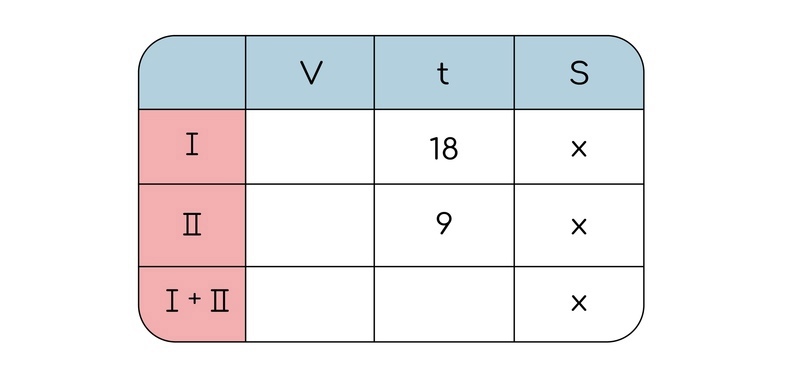
Теперь надо выразить производительность по формуле (через работу и время):

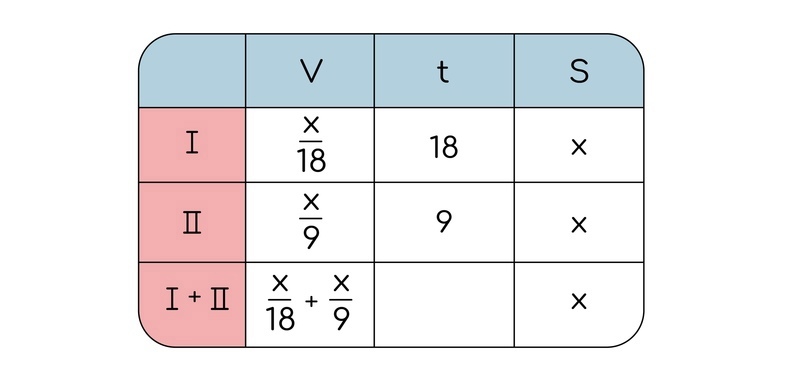
Дополнительно прописываем совместную производительность. Теперь, чтобы найти искомое время, нам надо работу поделить на производительность:

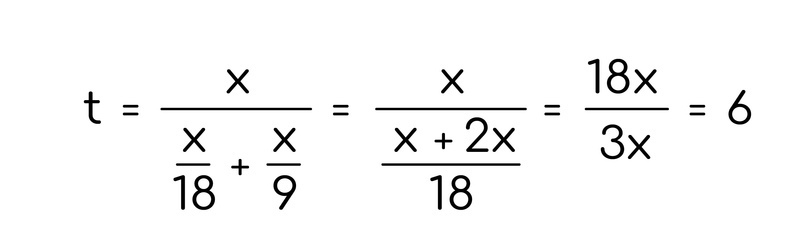
Так мы приходим к ответу. Но давайте посмотрим на то, что произошло с нашей переменной икс. ОНА СОКРАТИЛАСЬ!

А это означает, что нам не важно, чему равен этот икс. А это уже означает, что мы можем вместо икс брать вообще ЛЮБОЕ ЧИСЛО.

Значит можно было изначально взять удобное число, которое легко делить как на 18, так и на 9 (по сути ищем НОК):

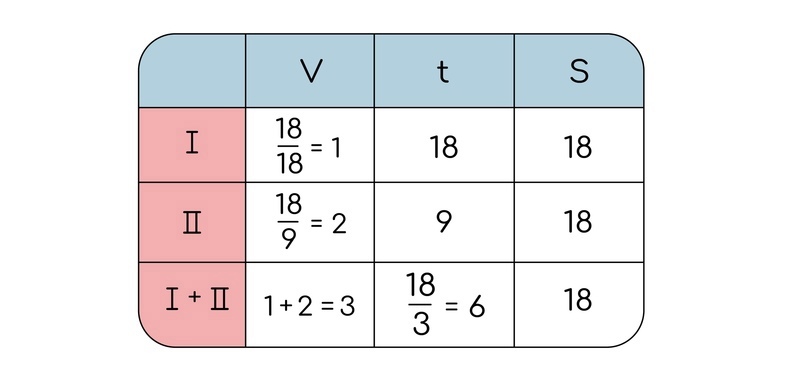
В таком случае нам даже с дробями не придется сталкиваться. Тут мы изначально выбрали удобное число для работы, которое приводит к таким же удобным значениям для производительности.

2) Получение уравнения через разность времени рабочих

Для начала составим таблицу:

Стоит сразу обговорить несколько принципов, которые позволят легче заполнить эту самую таблицу.

• Находим значение, которое точно можно записать без выражения через что-то другое (у нас это количество деталей 1-ого и 2-ого)
• Вводим переменную, читая вопрос задачи, и выражаем ту же величину другого объекта через эту переменную с использованием условия
• Написав два столбца, можем по общей формуле скорости, времени и пути выразить третий столбец

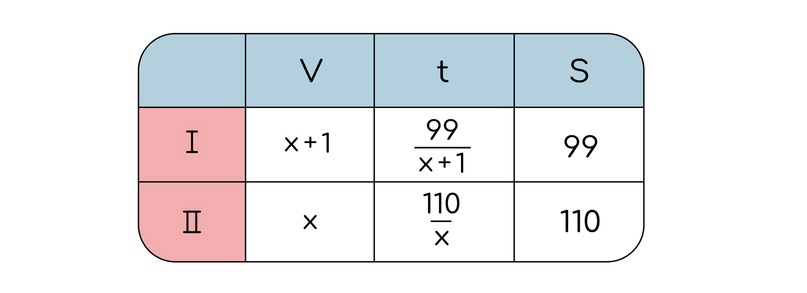
Теперь надо составить уравнение. Для этого чаще всего идут через время (или разницу во времени) двух объектов задачи.

Как не ошибиться в составлении уравнения?

Нам сказали, что первый тратит на 2 часа меньше, чем второй. Тогда можно сказать, что разница во времени первого и второго равна 2.

Теперь осталось правильно написать это утверждение в виде уравнения. Для этого мы должны из большего числа вычесть меньшее число. Если первый потратил меньше, то второй потратил больше. Значит из времени второго вычитаем время первого и приравниваем это к 2:

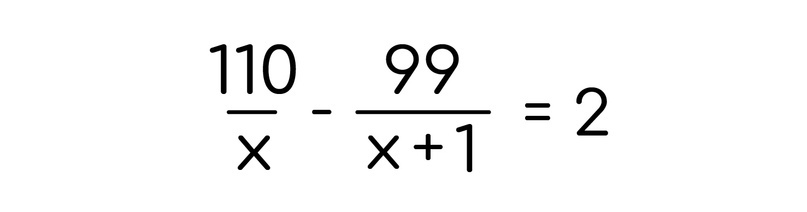
Если правильно составить уравнение, то дальше уже проблем не будет :)

Еще один полезный факт

Это задание первой части, а значит нет необходимости объяснять решение. Тогда можно подобрать корень. Почти всегда в ответе на такие задания появляются целые числа.

Более того, почти всегда сами дроби в уравнении тоже являются целыми числами. А значит нам надо подобрать такой икс, чтобы 110 на него делилось, а 99 делилось на икс + 1. Это число 10.

Проверяем:

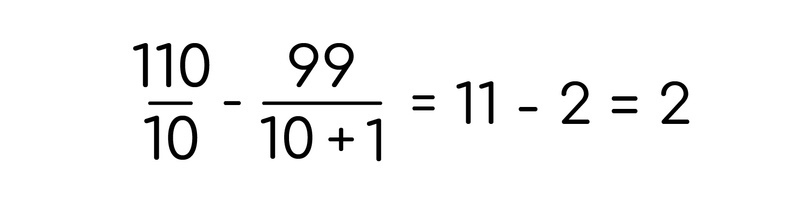
После подстановки мы видим, что уравнение превращается в верное равенство, а значит икс равное 10 является корнем нашего уравнения.

В целом можно выделить два таких глобальных прототипа заданий на производительность. В некоторых задачах могут быть докручены еще какие-то условия, но общая концепция будет сохраняться.