Окружность

1) Определение

Окружность — множество всех точек, равноудаленных от одной точки (центра).

У окружности есть различные элементы, которые необходимо знать. В первую очередь это радиус.

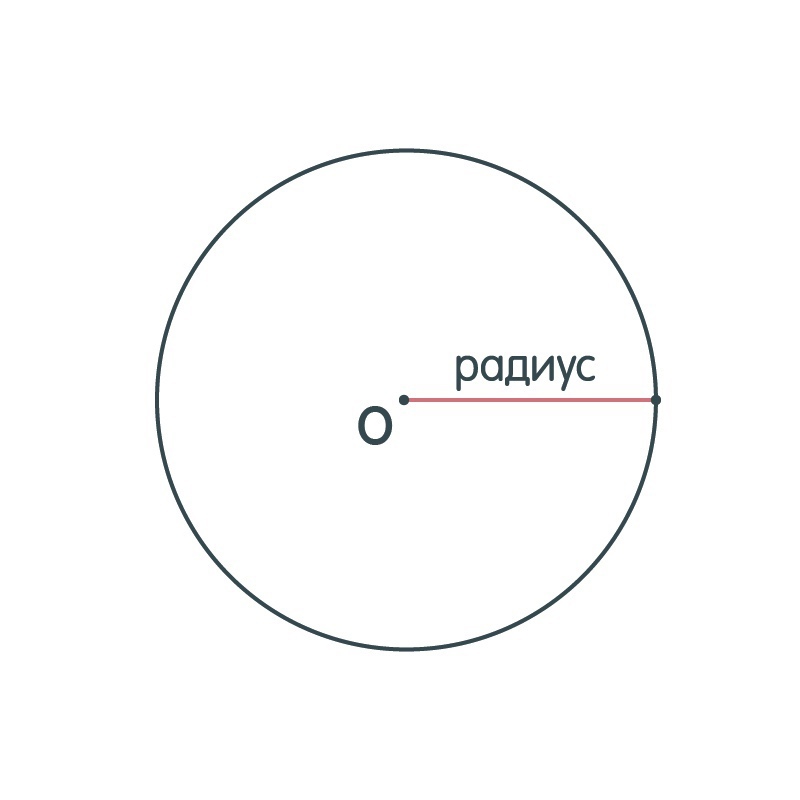
Радиус — это отрезок, соединяющий центр окружности с точкой на окружности. Также важно осознавать, что радиус является главным элементом, который будет фигурировать, можно сказать, во всех формулах, с помощью которых вычисляются различные параметры окружности (длина дуги, площадь). С помощью радиуса мы будем понимать размеры нашей окружности, с которой мы будем работать.

Также дополнительно стоит подробнее остановиться на определении окружности.

Дело в том, что иногда наличие окружности в задаче не будут формулировать напрямую в самом условии. Важно понимать, в каком случае мы можем самостоятельно сказать, что какие-то точки будут лежать на одной окружности.

Предлагаю посмотреть на рисунок ниже.

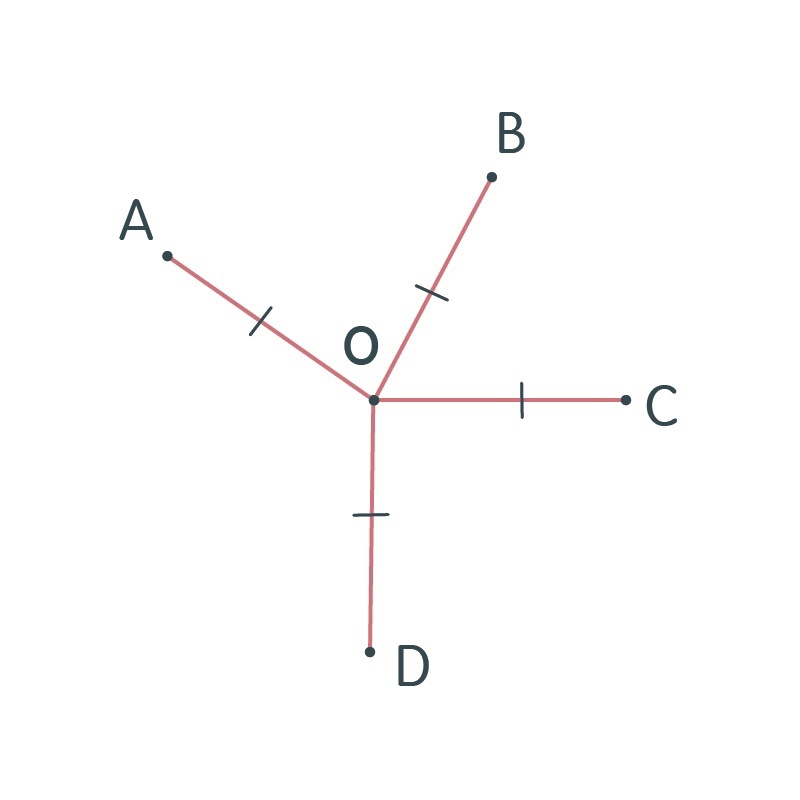
На этой картинке вы можете заметить, что точки A, B, C, D находятся на одинаковом расстоянии от точки О. В таком случае мы можем утверждать, что все эти 4 точки равноудалены от какого-то центра, а значит, лежат на одной окружности. В данной ситуации мы можем также утверждать, что все равные отрезки будут являться радиусами той окружности, которую мы будем рассматривать

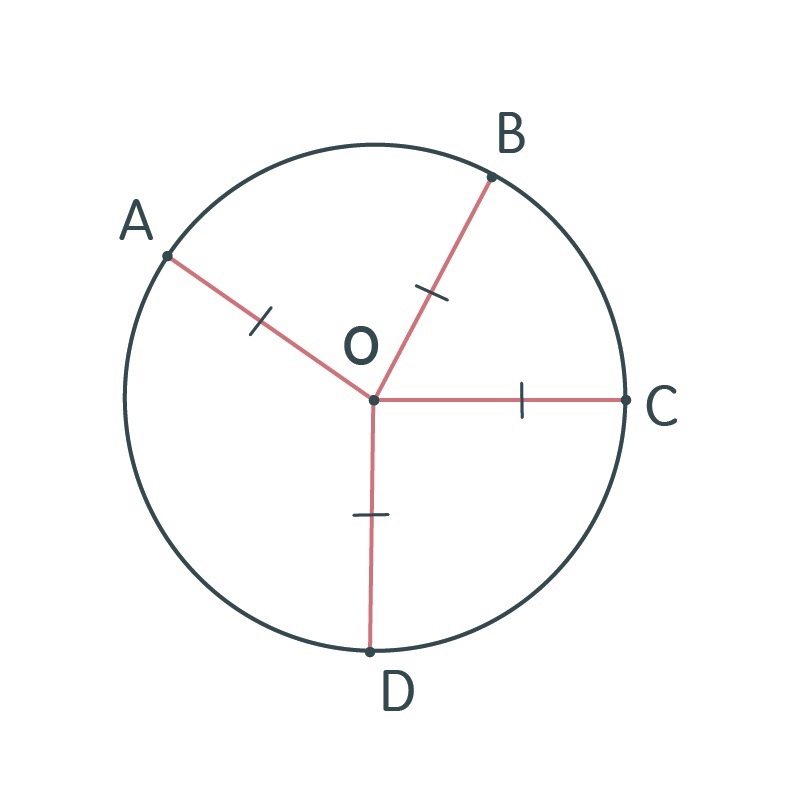
В любом случае вам пригодится понимание того, как можно «увидеть» наличие окружности, чтобы воспользоваться свойствами, связанными с этой фигурой.

2) Элементы окружности

Перейдем к оставшимся элементам окружности, с которыми нам тоже необходимо будет работать в задачах экзамена.

Хорда — отрезок, соединяющий две точки окружности.

Диаметр — хорда, проходящая через центр окружности. Также важно помнить, что диаметр по длине равен двум радиусам окружности.

Касательная — прямая, имеющая одну общую точку с окружностью (дальше подробнее рассмотрим факты, связанные с этим элементом, так как касательная супер часто появляется в заданиях экзамена).

Секущая — прямая, имеющая две общие точки с окружностью.

Нельзя также обойти стороной важные углы, которые необходимо рассматривать в заданиях на тему окружностей.

Конечно же речь идет о вписанных и центральных углах.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Центральный угол — угол, вершина которого лежит в центре окружности, а стороны также пересекают эту окружность.

Свойство про вписанные и центральные углы не очень сложное, но очень важное. Вписанный угол равен половине градусной меры дуги, на которую опирается, в то время как центральный — равен градусной мере дуги, на которую опирается.

То есть если возникнет ситуация, когда вписанный и центральный углы опираются на одну дугу, в таком случае центральный будет в два раза больше вписанного.

3) Свойства касательной.

Первое (и, пожалуй, наиболее встречающееся) свойство заключается в том, что радиус, проведенный в точку касания, перпендикулярен касательной.

Во всех задачах, где появляется касательная, так или иначе будет использоваться это свойство, поскольку наличие прямого угла дает информацию, которую мы сможем использовать дальше при нахождении спрашиваемых элементов.

Также относительно часто возникают ситуации, где проводят не одну, а две касательные из одной точки вне окружности. В таком случае мы должны уже смотреть немного на другие элементы. Сейчас все разберем :)

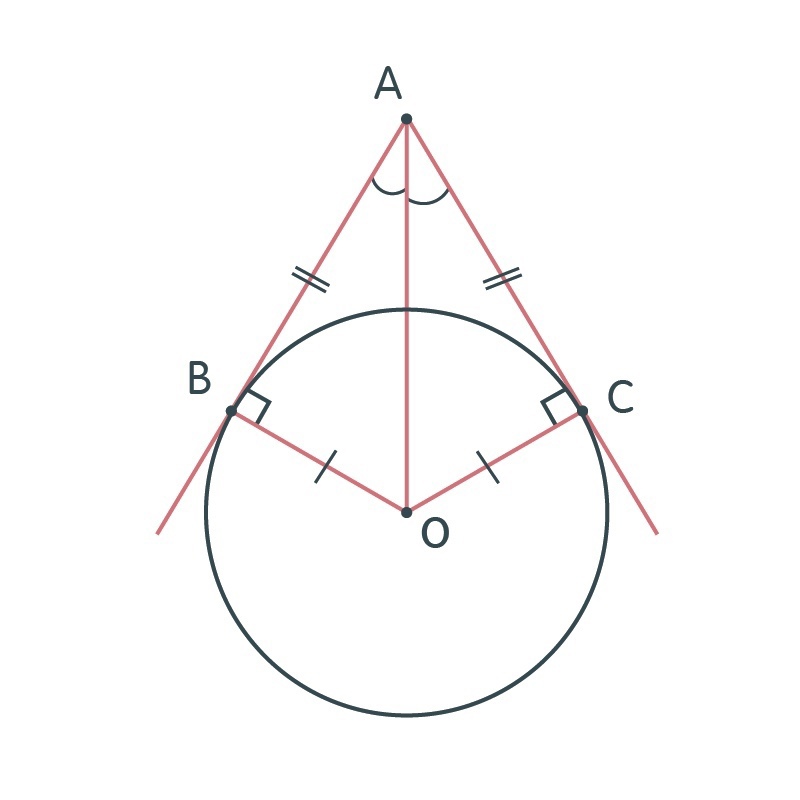
Если из одной точки проведены две касательные к окружности, то отрезки до точек касания равны.

Доказывается данное свойство не очень сложно. Необходимо рассмотреть два треугольника (в нашем случае АОВ и СОA). Они равны, так как равны радиусы, а гипотенуза является общей стороной (то есть равны по катету и гипотенузе).

Попробуйте вспомнить, почему этого достаточно для доказательства равенства прямоугольных треугольников.

Из равенства треугольников также следует, что отрезок АО является биссектрисой, так как верхние уголочки ВАО и САО равны.

Вы можете обратить внимание, что данная картинка очень похожа на ту, что была в разборе свойств биссектрисы. Там брали точку на биссектрисе угла и говорили, что она равноудалена от сторон угла. В том случае при желании тоже можно было разглядеть окружность.

Вообще из подобных картинок можно очередной раз сделать вывод о том, что очень многие темы математики (особенно геометрии) переплетаются друг с другом, а это значит, что если вы научитесь понимать эту связь, вы сможете самостоятельно выводить все необходимые для экзамена свойства.

4) Угол между касательной и хордой.

Данное свойство из тех, которые просто понять, но еще проще потерять и забыть. Вся проблема заключается в том, чтобы банально вспомнить это свойство.

Угол между хордой и касательной равен половине градусной меры дуги, стянутой этой хордой.

Однако еще чаще используется факт того, что угол между хордой и касательной равен вписанному углу, опирающемуся на дугу, стянутой этой хордой.

На рисунке вы можете заметить, что углы САВ, АDB и AEB равны друг другу, так как все они равны половине дуги АВ (вписанные углы равны половине дуги АВ, на которую они опираются, ну а угол САВ равен половине этой же дуги по свойству, которое мы описали выше).

Тема окружностей не просто так вызывает больше всего вопросов у школьников. Задачи на эту тему не очень часто встречаются на уроках, в основном все решают/проходят задачи на треугольники и четырехугольники.