Равнобедренный и равносторонний треугольники

В предыдущих статьях мы затрагивали виды треугольников, но говорили в основном о видах относительно углов. Сейчас будем затрагивать треугольники, обладающие особыми отличиями в рамках сторон.

1) Равнобедренный треугольник.

Равнобедренным является треугольник, у которого боковые стороны равны.

Что из этого следует?

а) Углы при основании равнобедренного треугольника равны.

Здесь стоит вспомнить взаимосвязь углов и сторон в рамках одного треугольника.

Напомню, что напротив большего угла лежит большая сторона. Напротив меньшего угла лежит меньшая сторона. Ну и напротив равных углов будут лежать равные стороны. Также верны и обратные факты.

В том числе поэтому можно сказать, что углы при основании должны быть равны.

б) Медиана, проведенная из вершины равнобедренного треугольника к основанию, также является биссектрисой и высотой.

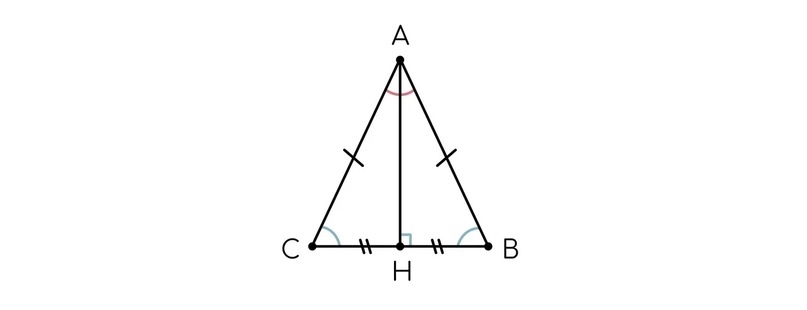
Достаточно часто в задачах на равнобедренные треугольники имеет смысл просвети данный особый элемент, поскольку он часто позволяет взглянуть по-другому на ту дополнительную информацию, которую вам дадут в условии задачи.

Вообще полезно попробовать самому доказать данное свойство.

Попробуйте рассмотреть два треугольника, которые здесь получились. Объясните, почему они равны. Как это поможет доказать, что проведенный отрезок АН будет не только (например) медианой, но и высотой и биссектрисой.

Поверьте, это хорошее упражнение на понимание геометрии.

2) Равносторонний треугольник

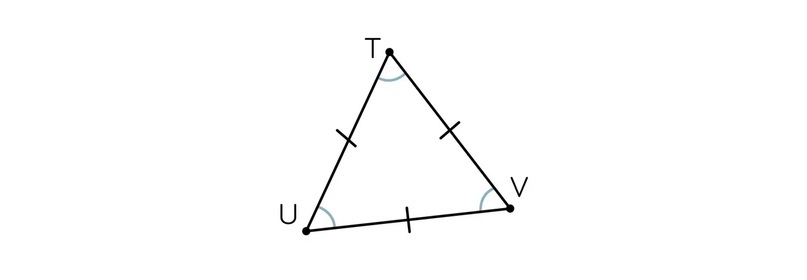
Равносторонний треугольник (правильный) — это треугольник, у которого все стороны равны.

Как и в случае с равнобедренным треугольником, мы можем утверждать, что напротив равных сторон лежат равные углы, а значит все углы в этом треугольнике тоже должны быть равны.

Так как сумма всех углов треугольника равна 180 градусам, значит каждый из них будет по 60.

К особенностям данного треугольника можно отнести то, что:

— любая медиана будет также являться биссектрисой и высотой

— все интересующие нас (с точки зрения распространенных задач экзамена) точки пересечения и центры вписанной и описанной окружностей будут совпадать.