Подсчет ребер и граней после преобразований в многогранниках

В заданиях по стереометрии в базовой математике могут попасться прототипы задач, где вершины многогранников отпиливают. Таким образом получаются новые многогранники с увеличенным количеством граней, вершин и ребер.

В этой статье мы разберемся в том, как происходит это увеличение.

Отпиливание вершины

Разбираемся на примере одной вершины

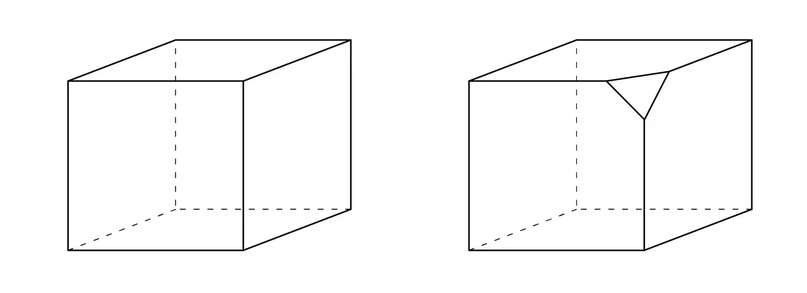
Рассмотрим куб, в котором отпилили одну вершину. Давайте посмотрим, что в таком случае изменилось.

• Вместо одной вершины появилось три (+2 вершины)
• Добавилась новая грань (+1 грань)
• Появилось 3 новых ребра (+3 ребра)

Если в задаче будут отпиливать все вершины, то вам необходимо просто к исходным значениям граней, ребер, вершин добавить новые соответствующие элементы, умноженные на количество отпиленных вершин.

Пример задачи

От деревянной правильной треугольной призмы отпилили все её вершины. Сколько ребер, граней и вершин у новой фигуры?

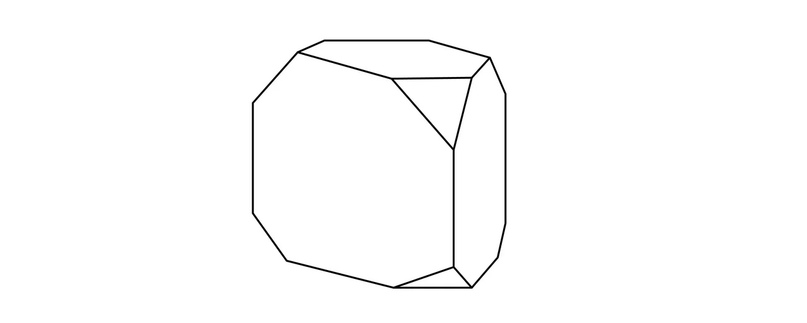
Давайте посчитаем, сколько вершин, ребер и граней в исходной правильной треугольной призме:

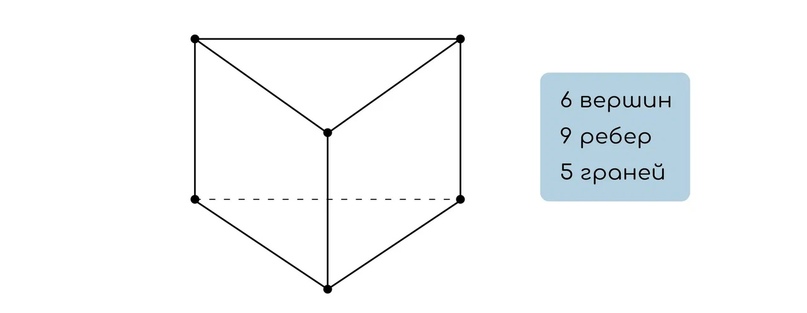
Тогда после отпиливания всех вершин мы получаем:

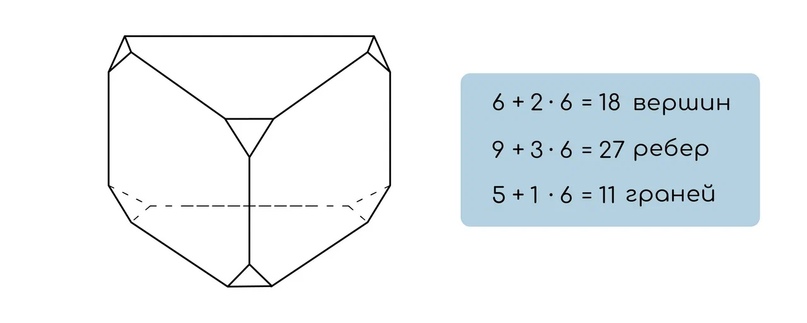
Вспоминаем, что после отпиливания одной вершины, у нас добавляется 2 вершины к изначальному количеству. Значит, после отпиливания 6 вершин, мы добавим 12.

С ребрами добавляем 6 раз по 3 (по итогу, 18 шт). Граней добавится столько, сколько вершин отпилили. В нашем случае это 6 шт.

По такой логике можно работать с любыми многогранниками, которые будут у вас на экзамене.