Тела вращения

В стереометрии вы можете встретить 3 типа тел вращения, которые могут вам попасться. Сейчас разберемся с каждым из них.

1) Цилиндр

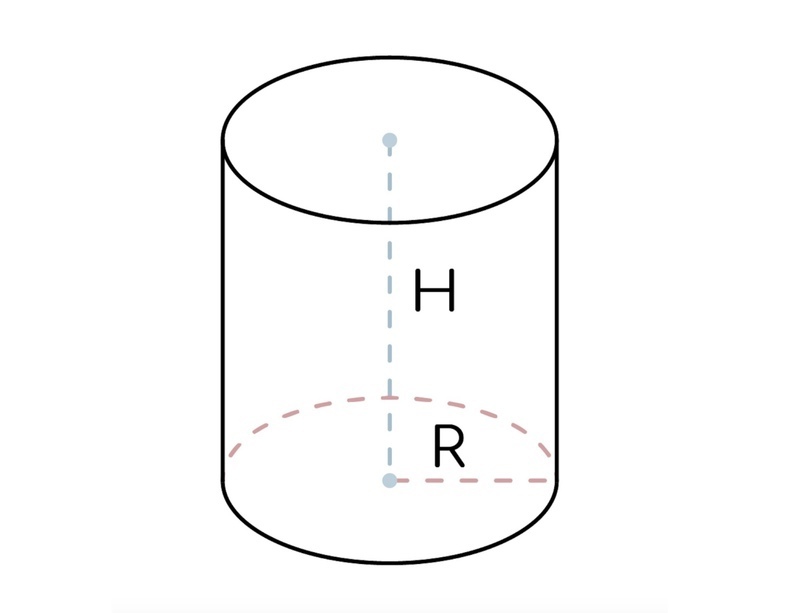
Эта объемная фигура получена вращением прямоугольника вокруг оси, проходящей через центр прямоугольника. Цилиндр имеет два круга в основаниях и образующую (то, что соединяет основания). Радиус основания – r, образующая цилиндра – h.

1.1 Объем цилиндра находится через произведения площади основания на высоту цилиндра. При этом стоит вспомнить, что площадь основания (площадь круга) находится как число пи, умноженное на квадрат радиуса. В таком случае мы получаем следующую формулу:

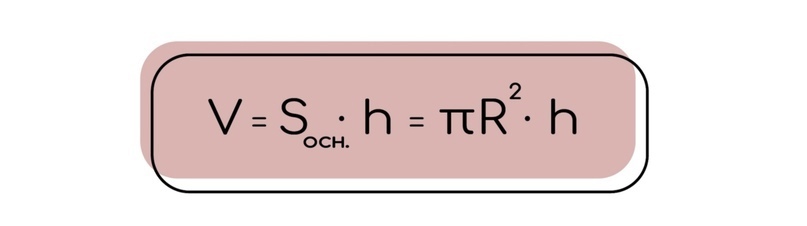
1.2 Для лучшего понимания того, как находится площадь боковой поверхности цилиндра, имеет смысл как бы «разрезать» цилиндр по образующей и расправить боковую часть. В таком случае мы получим прямоугольник, площадь которого мы уже умеем находить.

Одной стороной этого прямоугольника будет являться образующая (высота), а другой стороной будет являться дуга окружности.

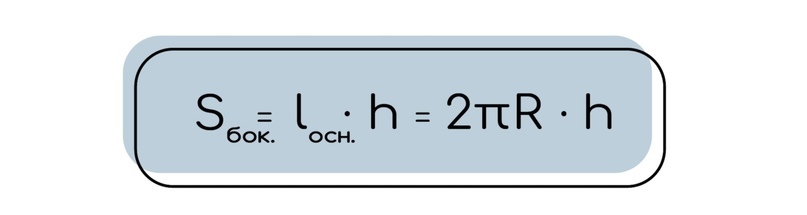
1.3 Чтобы найти полную площадь поверхности, необходимо просто к площади боковой прибавить две площади основания.

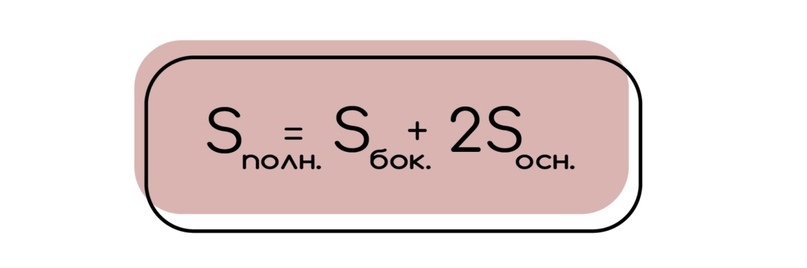
1.4 Осевое сечение цилиндра проходит через ось цилиндра и перпендикулярно плоскостям оснований. В сечении получается прямоугольник, одна сторона которого будет образующей (высотой), а другая будет диаметром.

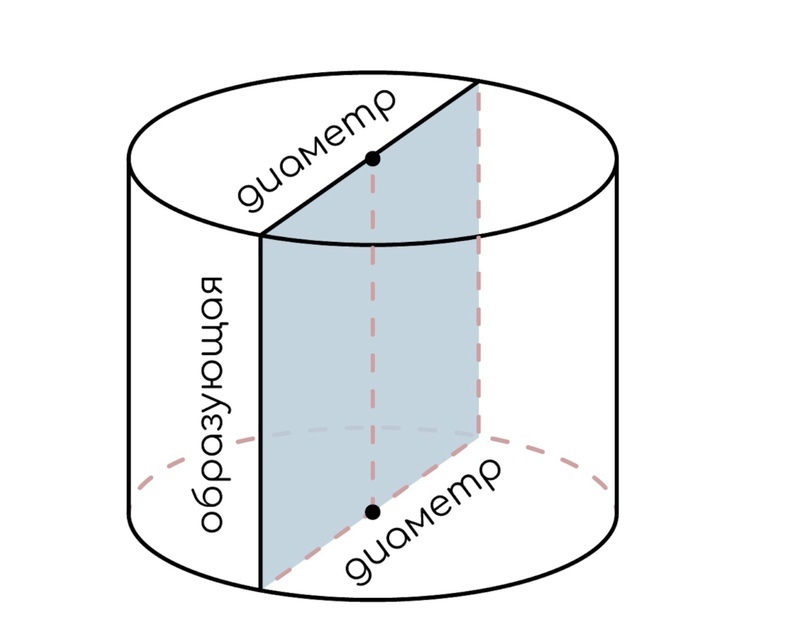
В некоторых задачах могут попросить найти площадь этого сечения. Или могут попросить выразить площадь боковой поверхности через площадь данного сечения.

Это возможно, так как в формуле площади данного сечения уже будут содержаться высота и радиус основания.

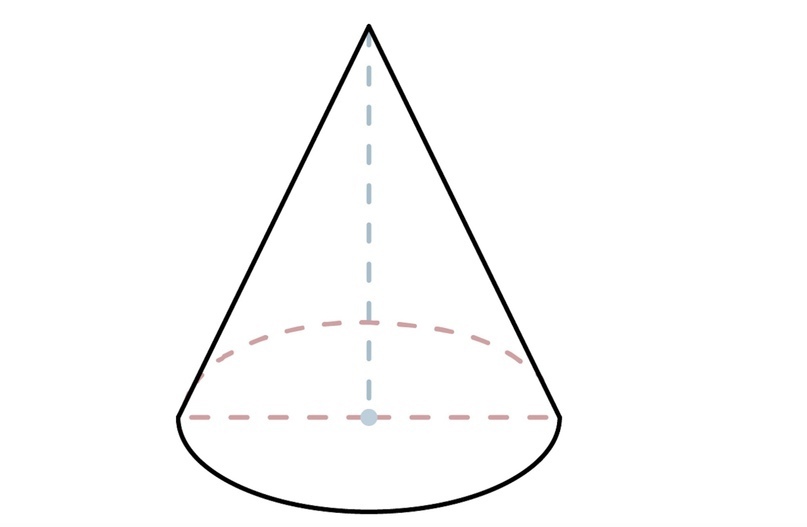
2) Конус

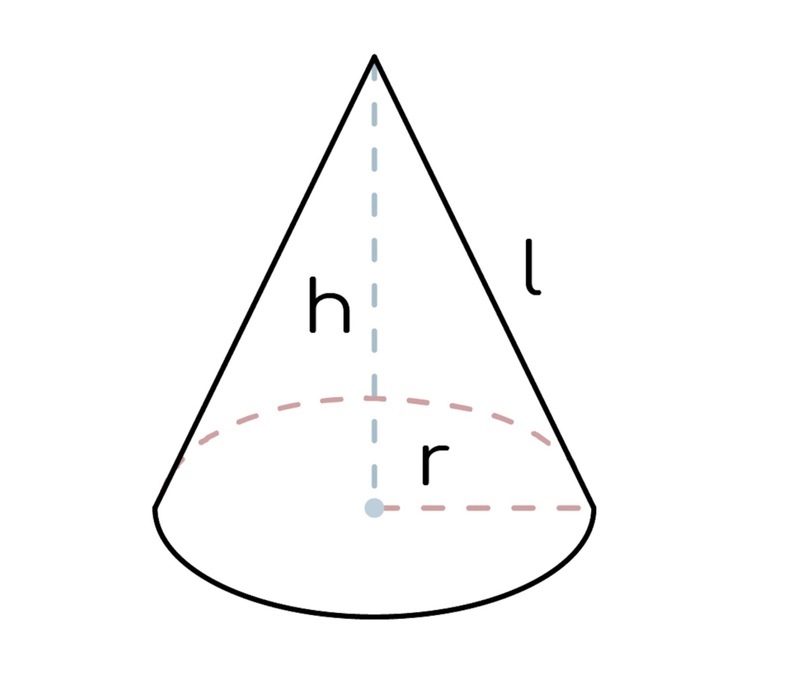
Эта объемная фигура получена путем вращения прямоугольного треугольника вокруг одного из своих катетов. Образующая — l, высота — h , радиус основания — r.

2.1 Объем конуса похож на формулу объема пирамиды. Там также присутствует коэффициент 1/3. Площадь основания находится через формулу площади круга. Эту формулу мы вспоминали выше на примере объема цилиндра.

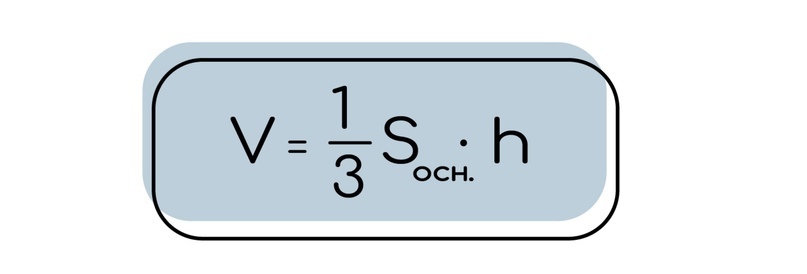
2.2 С площадью боковой поверхности все обстоит гораздо интереснее. Здесь тоже имеет смысл «разрезать» конус по образующей. В таком случае при развертке получится сектор некоторой окружности с радиусом, который равен образующей.

И теперь при нахождении площади сектора мы должны понять, какую часть от всего этого круга с радиусом l (равен образующей) занимает наш сектор. Для этого мы должны найти отношение дуги сектора (которая равна по сути длине дуги основания конуса) к длине окружности с радиусом l (равен образующей) и умножить его на площадь круга с радиусом l (равен образующей).

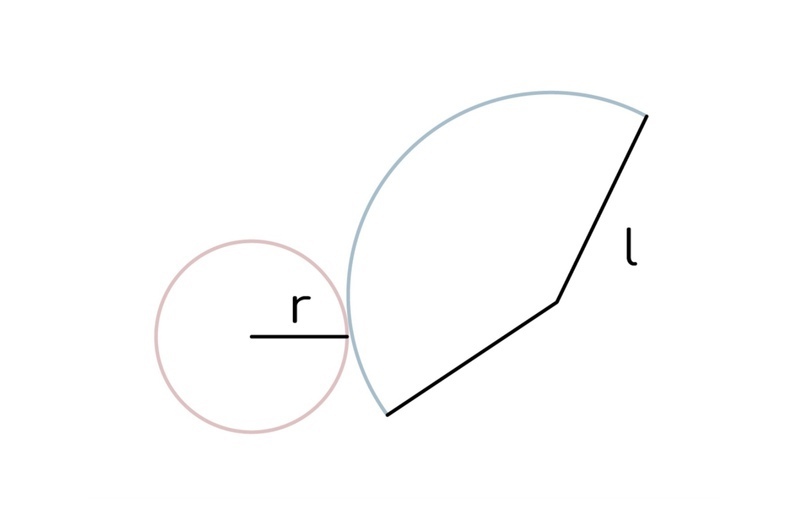
По итогу после всех преобразований получим вот такую формулу:

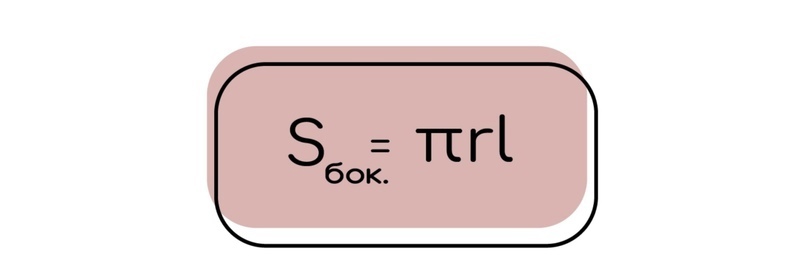
2.3 Площадь всей поверхности будет находиться как сумма площади боковой поверхности и площади основания:

2.4 Осевое сечение конуса представляет собой равнобедренный треугольник, боковые стороны которого являются образующими конуса, а основание — диаметр основания конуса.

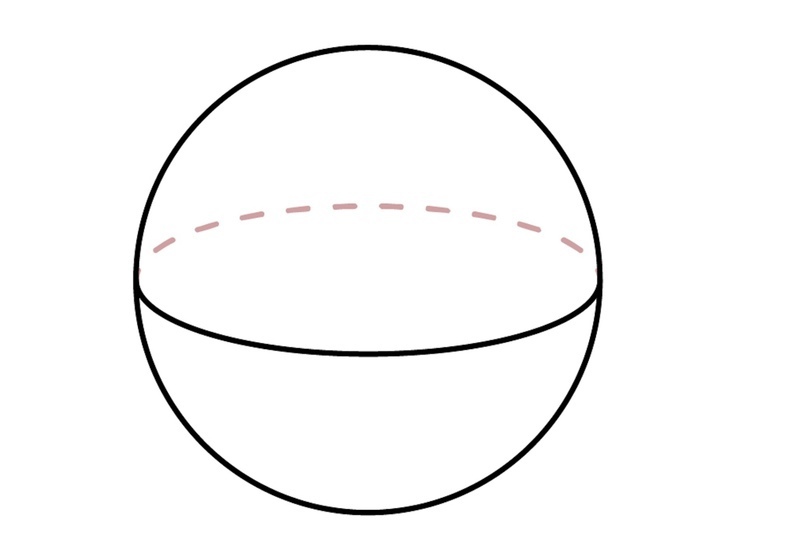
3) Шар/сфера

Шар (заполненный внутри) – это геометрическое тело, ограниченное поверхностью, все точки которой отстоят на равном расстоянии от центра.

Сфера (пустая внутри) – поверхность, образованная вращением контура.

Важно осознать, что радиус — единственная величина, от которой зависят объем и площадь поверхности шара.

Так как площадь является квадратичной величиной, а объем — кубической, в каждой из этих формул будет присутствовать радиус в квадрате и радиус в кубе соответственно. Также там будет везде число пи. Останется только запомнить коэффициенты для каждой из этих формул.

3.1 Объем шара:

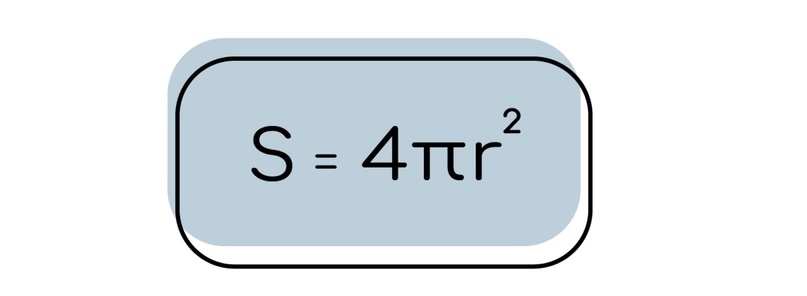
3.2 Площадь поверхности:

3.3 Из сечений важно запомнить формулировку «большая окружность шара/сферы», которая подразумевает окружность, радиус которой равен радиусу шара/сферы.