Пирамиды

Пирамида — многогранник, одна из граней которого — произвольный многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Правильная пирамида – пирамида, в основании которой лежит правильный многоугольник, высота падает в его центр, а боковыми гранями являются равные равнобедренные треугольники.

Правильный тетраэдр – это треугольная пирамида, все грани которой – равные равносторонние треугольники.

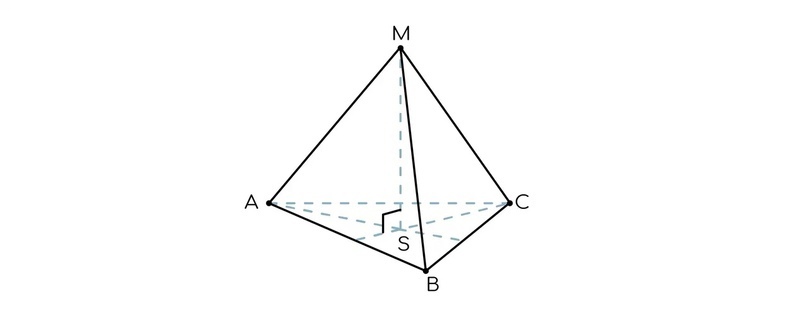
В базовой математике почти во всех задачах вы будете встречать именно правильные пирамиды, что облегчает некоторое понимание идей, которые необходимо будет использовать в подобных заданиях.

Дополнительно давайте разберемся в том, какими свойствами обладают пирамиды, боковые ребра которых равны.

Если боковые ребра пирамиды равны, то высота падает в центр описанной окружности.

Попробуйте провести высоту. Точку, в которую упала высота необходимо соединить с вершинами основания. В таком случае вы получите равные прямоугольные треугольники (по гипотенузе и общему катету).

Тогда оказывается, что отрезки до вершин равны, а значит, вершины равноудалены от этой точки, в которую падает высота. Отсюда следует, что эта точка является центром окружности, которая проходит через вершины основания.

1) Объем пирамиды находится по формуле

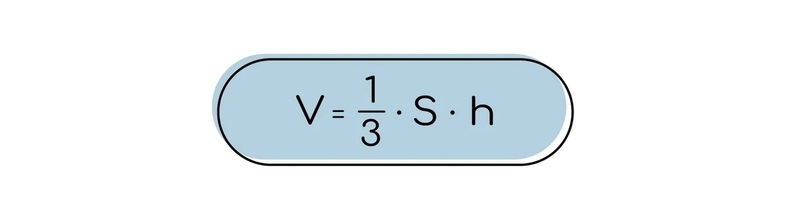
2) Площадь боковой поверхности можно найти как сумму площадей боковых граней, однако если речь идет о правильной пирамиде, то можно найти площадь одной грани и умножить на их количество.

Здесь также стоит вспомнить особый элемент в боковых гранях пирамиды.

Апофема – высота боковой грани пирамиды.

3) Чтобы найти площадь всей поверхности пирамиды, нам необходимо к площади боковой поверхности прибавить площадь основания.