Призмы
Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.
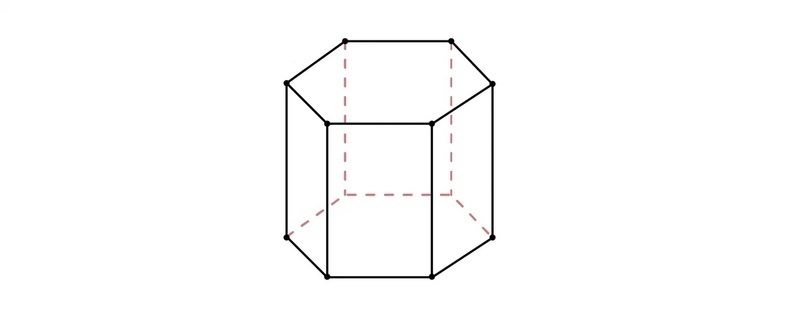
В зависимости от того, какой многоугольник лежит в основании, мы получаем разные названия призм.
Треугольная призма — в основаниях треугольники.
Четырехугольная призма — в основании четырехугольник (и так далее).
Также разделяют прямые и наклонные призмы.
Наклонная призма — призма, боковые грани которой находятся не под прямым углом к основанию.
Прямая призма — призма, боковые грани которой перпендикулярны основаниям (боковые ребра перпендикулярны основаниям).
Правильная призма — это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы — равные прямоугольники.
То есть в правильной треугольной призме в основании правильный треугольник, а боковые ребра перпендикулярны основаниям.
В правильной четырехугольной призме в основании лежит квадрат, а боковые ребра перпендикулярны основаниями (и так далее).
В рамках заданий экзамена ЕГЭ мы будем встречать особые виды призм. Один из видов призм, с которыми придется достаточно часто встречаться — параллелепипед.
Параллелепипед — призма, грани которой являются параллелограммами.
Прямой параллелепипед — призма, основания которой являются параллелограммами, а боковые грани — прямоугольниками.
Прямоугольный параллелепипед — призма, все грани которой являются прямоугольниками.
Куб — призма, все грани которой являются квадратами.
Что у вас могут попросить вычислить в подобных заданиях?
1) Площадь боковой поверхности призмы.
Площадь боковой поверхности можно найти как сумму площадей боковых граней. Однако можно воспользоваться формулой:
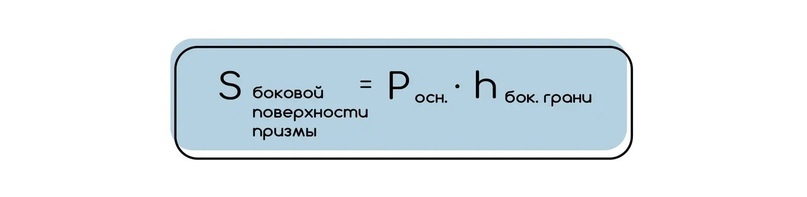
Эту формулу можно получить при вынесении общей высоты, когда мы рассматриваем сумму площадей боковых граней (там получаются параллелограммы, площадь которых можно найти через произведения оснований на высоту). Вынеся этот общий множитель, получаем в скобочках сумму сторон основания, которую как раз можно назвать периметром.
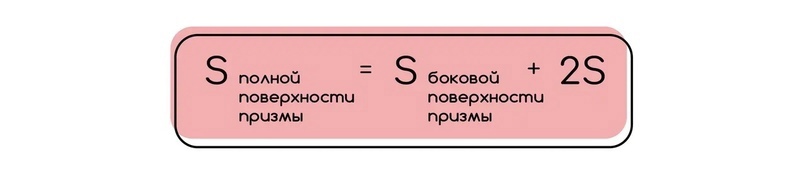
2) Площадь всей поверхности призмы.
Чтобы найти площадь всей поверхности призмы, необходимо к площади боковой поверхности добавить две площади основания.
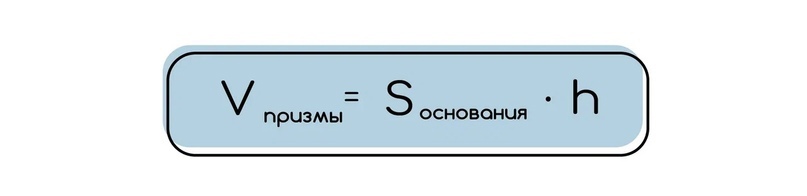
3) Объем призмы.
Куда же без объема в стереометрии. Формула объема не очень сложная: