Углы на тригонометрической окружности

В тригонометрии вам предстоит много работать с единичной (радиус равен 1) окружностью, оси которой будут называться sinx и cosx.

Объяснение того, что тут забыла окружность, можно найти в самом тригонометрическом тождестве. Оно является уравнением окружности :)

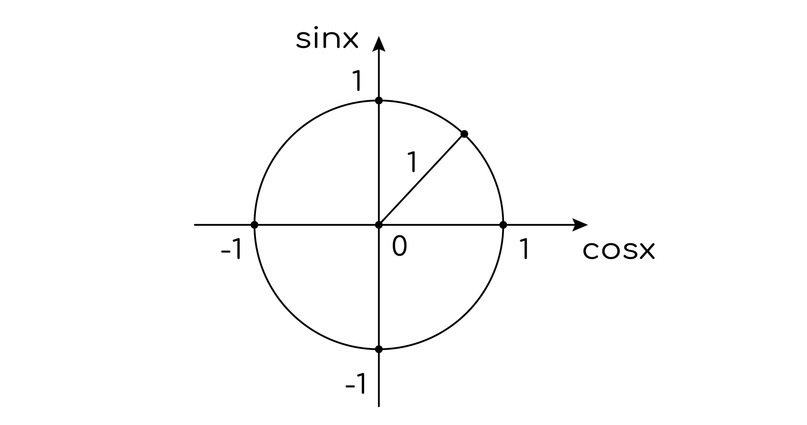
Для нас важно понять, каким образом на окружности будут отмечаться углы, тригонометрические значения которых мы будем с вами находить.

Тут есть два способа показать этот угол.

Также можно сказать, что существует два способа указать местоположение точки на окружности, так как в дальнейшем мы увидим, что можно брать углы больше 360 градусов, но при этом местоположение точек на окружности меняться не будет. Из-за этого и значения тригонометрических функций меняться тоже не будут.

Угол в градусах

Для начала стоит понять, что угол в градусах будет формироваться через угол между осью абсцисс и радиусом, который мы будем поворачивать на этот угол.

Так как это угол, вершина которого будет выходить из центра окружности, то такой угол можно назвать центральным. Отсюда следует, что дуга, на которую он будет опираться, будет равна значению этого центрального угла в градусах.

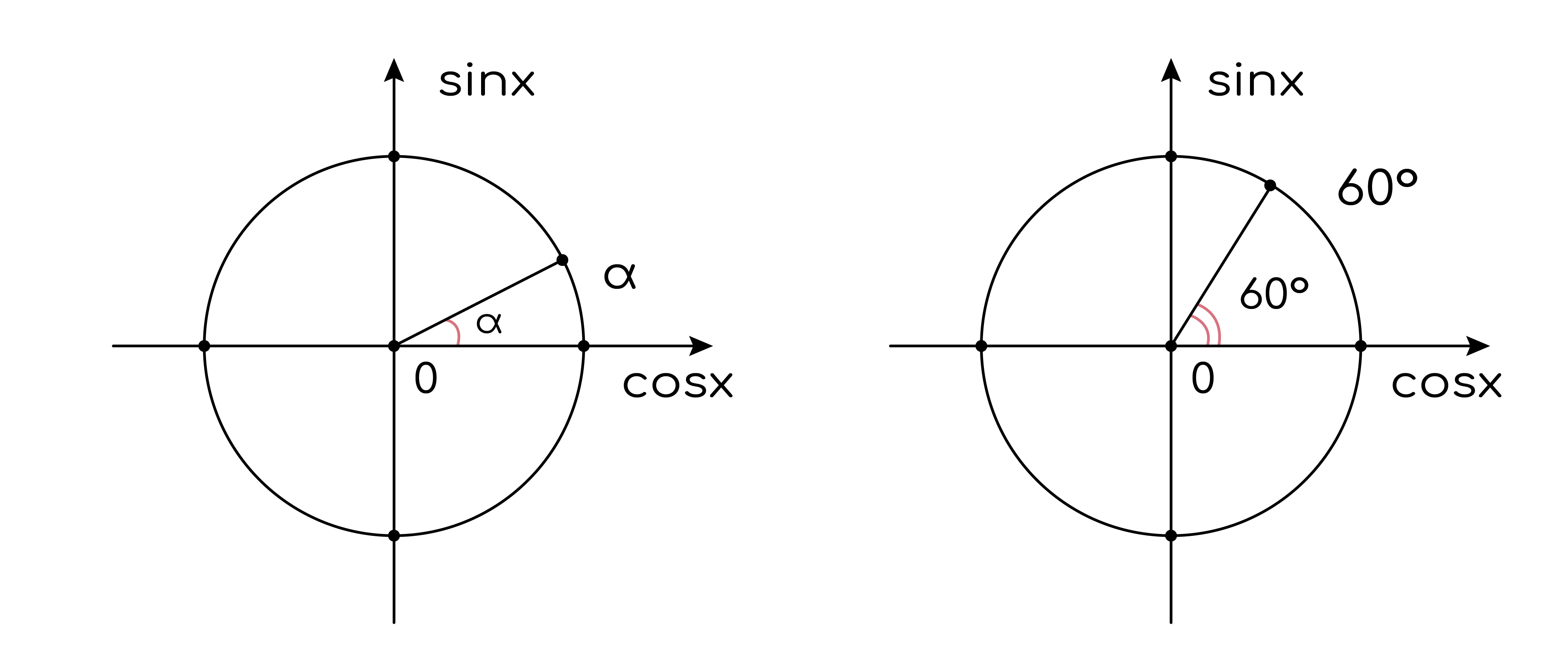
Угол в радианах (через π)

В точку на окружности можно попасть не только через поворот радиуса на какой-то градус, но и через прохождение некоторого расстояния по самой дуге.

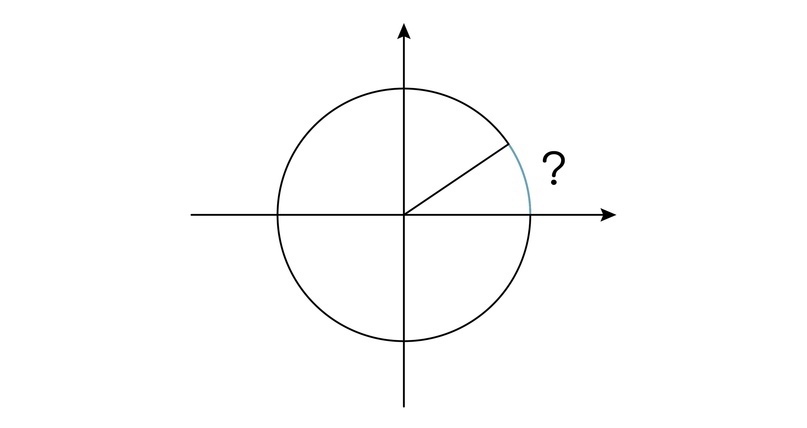
Осталось понять, как найти это расстояние.

Для начала давайте вспомним, по какой формуле ищется длина окружности:

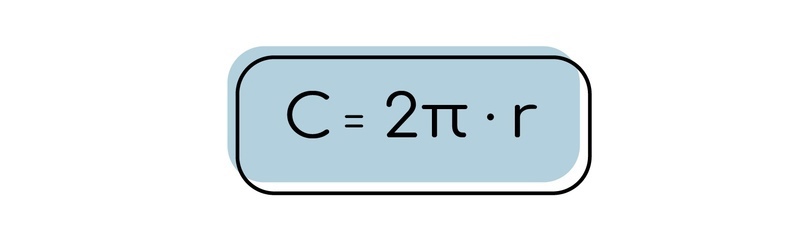
Но радиус конкретно нашей тригонометрической окружности равен 1, и тогда мы можем сказать, что длина нашей окружности равна 2π (если в формулу радиус подставить).

Теперь выходит так, что если мы пройдем по дуге расстояние 2π, то попадем в ту же точку, как если бы мы поворачивали радиус на 360 градусов.

Тогда, пройдя расстояние π, мы как будто повернем радиус на 180 градусов.

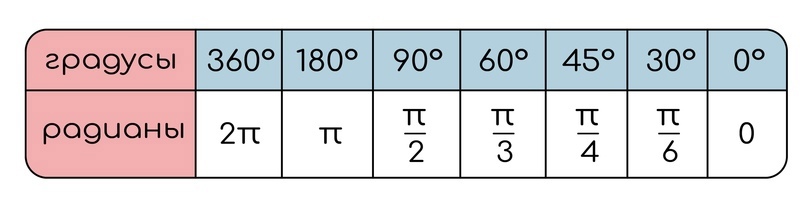
Тогда для любого угла можно сопоставить то расстояние, которое необходимо пройти по дуге. Вот примеры для табличных значений:

Направления углов

Стоит еще добавить, что мы можем двигаться в разных направлениях с точки зрения углов.

• Если мы движемся против часовой стрелки, то углы будут со знаком «+»

• Если по часовой — то со знаком «-»