Определение логарифма

Перед тем как пререходить к формулам, стоит вспомнить, что такое логарфим, откуда он берется, и какие ограничения стоит накладывать на выражения внутри логарифма.

Ограничения на показательные уравнения

Сперва рассмотрим следующее показательное уравнение:

Также стоит вспомнить, какие ограничения накладываются при рассмотрении показательных уравнений.

1) Основание должно быть больше нуля.

Если рассмотреть функцию с отрицательным основанием (например -2), то при значении икс равном 0,5, мы имеем в виду, что будем извлекать корень из -2, что в рамках действительных чисел невозможно.

У нуля есть пробелемы при возведении в отрицательную степень, поэтому мы тоже не можем рассматривать ноль как основание на области всех действительных чисел для показателя степени.

Именно поэтому мы рассматриваем в рамках таких уравнений только основания, которые больше нуля.

P.S. Это не значит, что мы не можем отрицательные числа возводить в какие-то степени. Разговор лишь о том, что в рамках показательных уравнений мы этого делать не будем.

2) Само выражение в некоторой степени должно быть больше нуля.

Попробуйте подставлять различные степени на области действительных чисел и вы убедитесь, что невозможно возвести положительное основание в такую степень, чтобы результат возведения был меньше или равен нулю.

А если наше положительное основание в какой-то степени больше нуля, то и выражение справа (так как оно равно выражению слева) тоже должно быть больше нуля.

По итогу приходим к следующему:

Когда мы разобрались с ограничениями на показательные уравнения, мы готовы переходить к логарифмам :)

Определение логарифма

Для начала давайте попробуем проговорить, что такое икс в данном уравнении, которое мы с вами записывали.

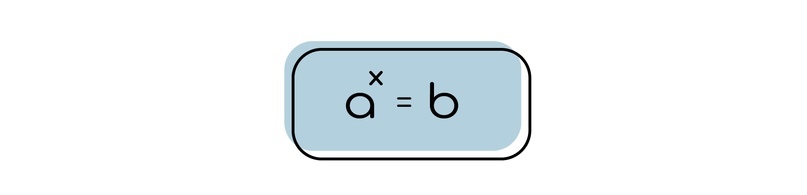
Х — это такой показатель степени, в который нужно возвести основание a, чтобы получилось число b.

А теперь показатель степени переводим на математический язык, называя это логарифмом. И тогда получается, что х — это логарифм b по основанию а.

Ограничения на внутренние выражения логарифма

Обратите внимание, что логарифм появляется из показательного уравнения, значит ограничения на показательные уравнения сохранятся и для логарифмов. Однако к нам добавится еще одно ограничения на основание.

Рассмотрим следующее уравнение:

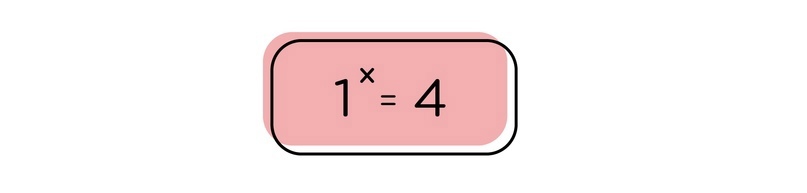
Мы помним, что 1 в любой степени должно равняться 1. Это означается, что в этом уравнении нет решений, а значит и невозможно сказать, что икс - это такая степень, в которую нужно возвести основание 1, чтобы получилось число 4, потому что такой степени не существует.

Теперь давайте рассмотрим вот такое уравнение:

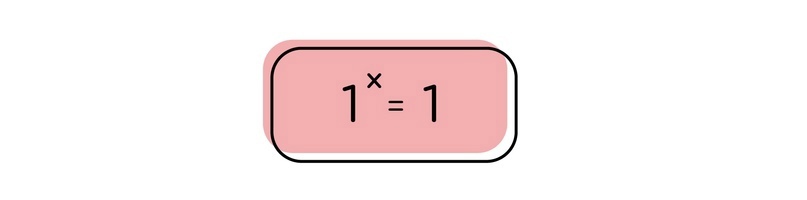
В этом случае икс будет любым. Но тогда, говоря о том, что икс — это такая степень, в которую нужно возвести основание 1, чтобы получилось число 1, мы будем иметь в виду абсолютно любое число, что не очень вяжется с будущей работой с логарифмами.

По итогу получается, что в рамках показательных уравнений основание может быть единицей, но в рамках логарфима это не будет иметь смысла. Поэтому мы дополнительно говорим о том, что основание логарифма не равняется единице.

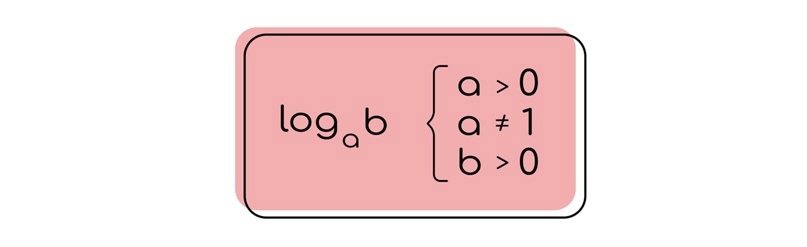
Использование определение логарифма для решения уравнений

Стоит также осознать, что мы всегда получаем логарифм при решении показательных уравнений, просто значения некоторых из них мы знаем.

Давайте рассмотрим несколько примеров:

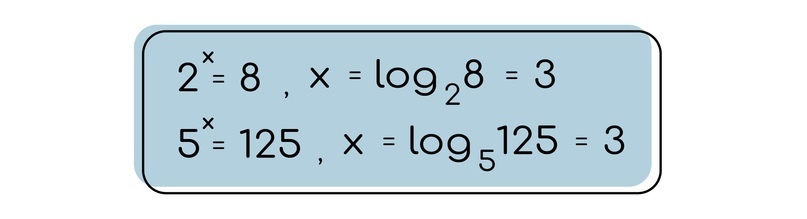
В рассмотренных выше случаях мы могли сразу назвать икс, но, по-хорошему, мы пропускали этап написания логарифма, однако в некоторых случаях мы не можем назвать значение икс, так как оно будет явно нецелым.

В данных примерах нам необходимо как-то записать степень, именно поэтому она будет прописываться через логарифм.

Примеры вычисления логарифмов

Чтобы лучше прочувствовать определение и смысл логарифма, давайте напишем несколько отдельных логарифмов и попытаемся получить значения, которым они будут равны.

Увидев такой логарифм мы мысленно говорим, что перед нами такая степень, в которую нужно возвести основание 3, чтобы получилось число 81, поэтому такая степень равна 4.

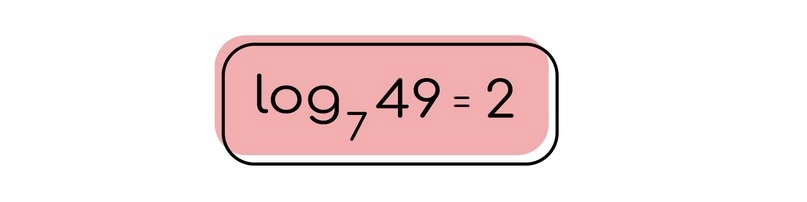
Здесь мы видим, что перед нами такая степень, в которую нужно возвести основание 7, чтобы получилось число 49. Эта степень равна 2.

Давайте рассмотрим пример чуть посложнее.

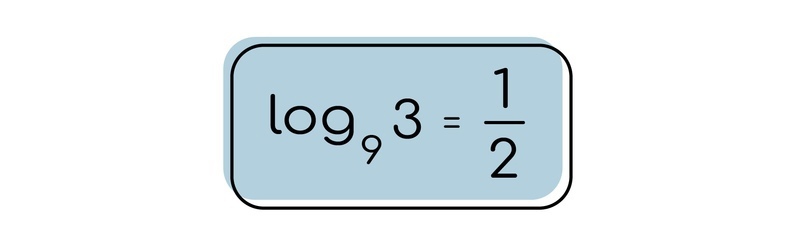
Перед нами такая степень, в которую нужно возвести основание 9, чтобы получилось число 3. Обычно мы извлекаем корень из 9, чтобы получить число 3, но корень — это какая степень? Как раз ½.

Здесь мы рассмотрели всю основную информацию, которую необходимо осознать про логарифм, чтобы понять все последующие формулы, которые мы будем использовать при решении заданий!