Уравнение Менделеева-Клапейрона. ОГЗ. Изопроцессы.

Уравнение Менделеева-Клапейрона

Есть законы, без которых даже заходить на ЕГЭ по физике не стоит. Это один из них. И все дело в большом количестве величин, которые связывает это уравнение. Получить его можно из формулы, которую мы уже использовали в предыдущей статье (p=nkT):

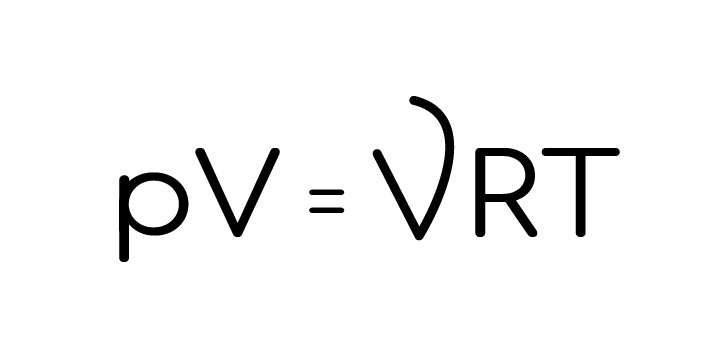
Оно связывает все параметры, определяющие состояние газа: давление, объем, температуру. Поэтому оно постоянно используется в разных задачах, и не надейся не встретиться с ним в ЕГЭ, при чем и в первой, и во второй части.

Кстати без предыдущей статьи тут делать нечего, машина без двигателя не поедет.

Хитрость, которая ломает судьбы бедных школьников, когда в задаче на молекулярку просят найти плотность, а в уравнении Менделеева-Клапейрона ее нет.

Не горячись. Сейчас покажу как ее легко там сделать. Коротенький вывод:

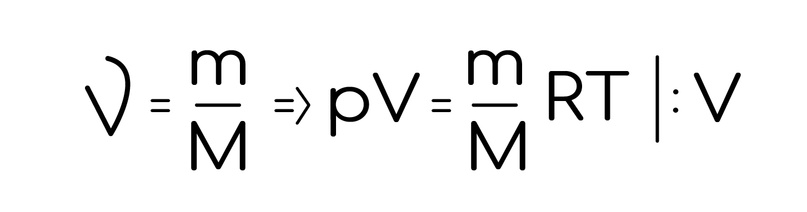
И вспоминая еще одну до невозможности важную формулу, которая попадается везде (по секрету, это про массу, которая равна плотности, умноженной на объем) мы получаем:

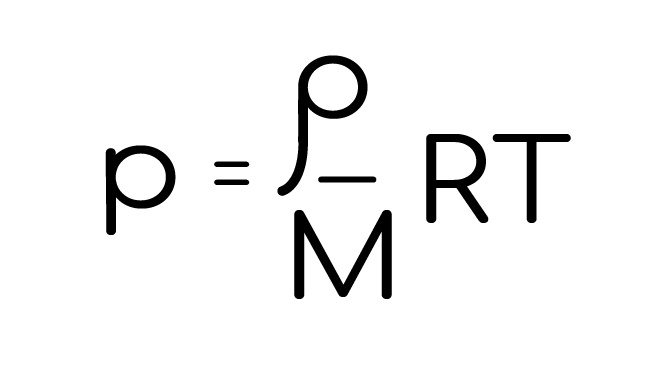
Откуда ты и выразишь искомую плотность. Броо, да мы дрим тим, едем дальше.

Объединенный газовый закон

А теперь то, что вывел господин Клапейрон на основе уравнения. Состояние газа, как мы говорили, описывается через давление, температуру и объем. А это соотношение, остается постоянным для ДАННОГО количества газа при любом наборе этих величин:

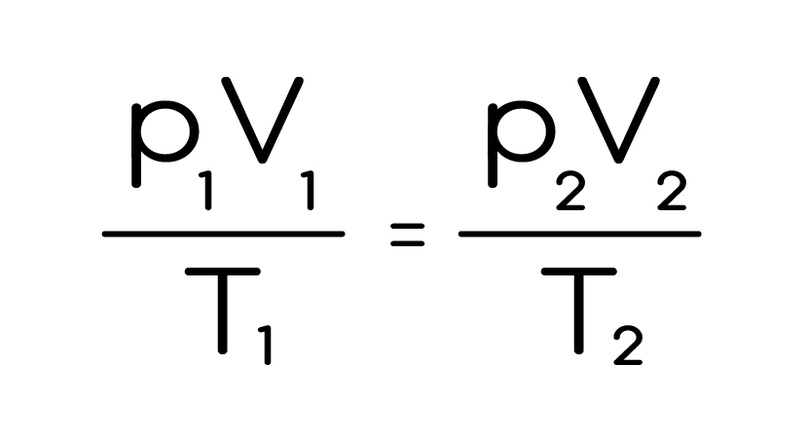
А теперь внимательно послушай:

Это и предыдущее уравнение (Менделеева-Клапейрона) ни в коем случае нельзя забывать, при решении задач всего раздела молекулярной физики.

Как в первой, так и во второй части, эти формулы встретятся в любом варианте ЕГЭ, будь к этому готов.

Но часто при переводе газа из одного состояния в другое, меняются не все три величины сразу, какая-то из них может оставаться без изменения.

Изопроцессы

Да, задачи делают специально такие, чтобы одна из переменных была константой (хотя и в жизни такие процессы очень распространены). Например, нагревают газ, а объем при этом увеличивается так, что давление остается постоянным. Или тот же газ нагревают, но в закрытом жестком сосуде, так что повышается давление, а объем поменяться уже не может.

Изобарный процесс

Так как сейчас в ЕГЭ могут попадаться вопросы с фамилиями умников, которые выводили эти законы, придется их тоже давать.

Закон Гей-Люссака – изменение состояния при постоянном давлении:

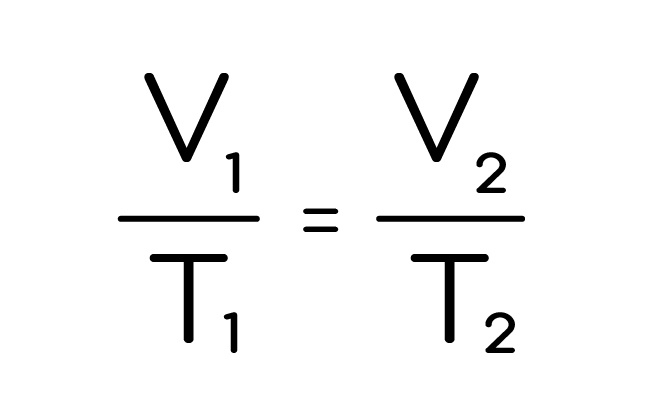
Логика, кстати, простая, я бы тоже так уравнения хотел открывать: взять объединенный газовый закон, при постоянной p ее можно просто сократить и получится изобарный процесс. Так будет и с остальными переменными.

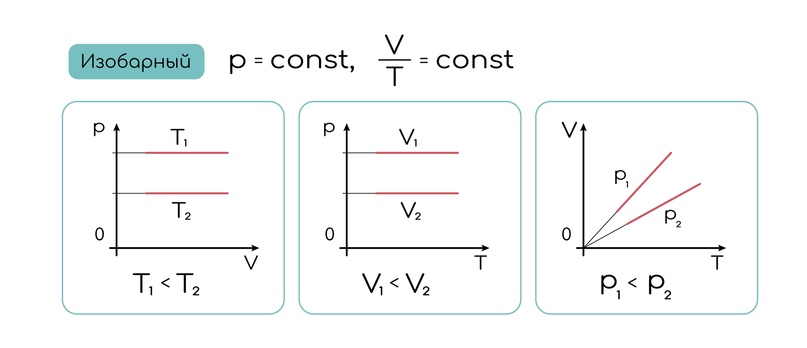
Полезно видеть и графики этих процессов, они тоже часто мелькают. Вот так выглядит изобара в разных системах координат. Если хорошо все с математикой, то эти графики покажутся совсем простыми и логичными. Обрати внимание, что наклонные графики обязательно проходят через ноль:

Изохорный процесс

Закон Шарля – изменение состояния газа при постоянном объеме. Все также, он просто вычеркнул постоянный объем из того же закона и получил свой:

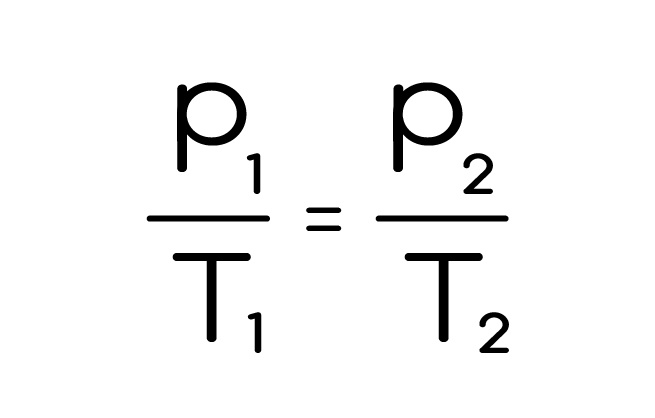
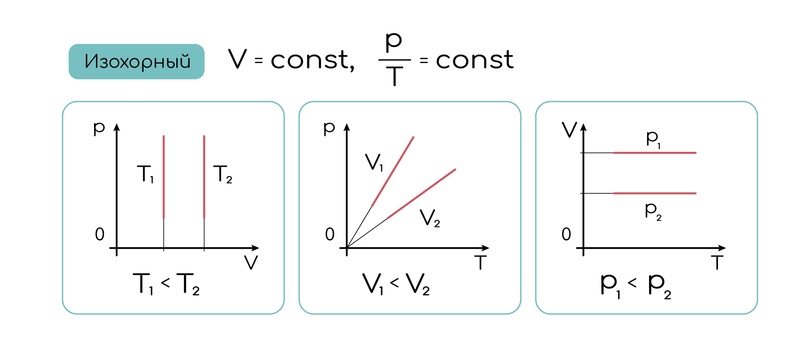
Графики изохоры в различных координатах:

Изотермический процесс

Закон Бойля-Мариотта – изменение состояния газа при постоянной температуре. Они тоже не были оригинальными и просто убрали постоянную температуру и получили:

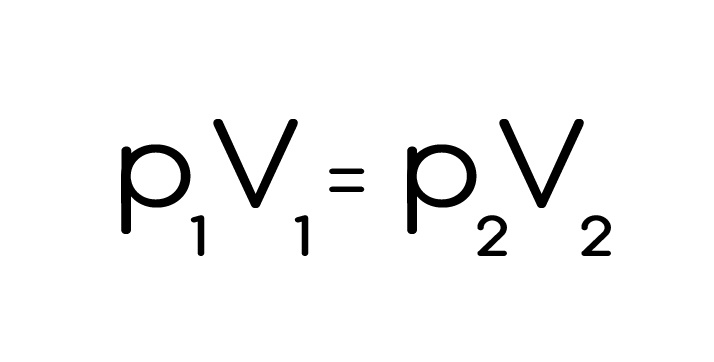
Так как тут температура была в знаменателе, то график изотермы будет интереснее:

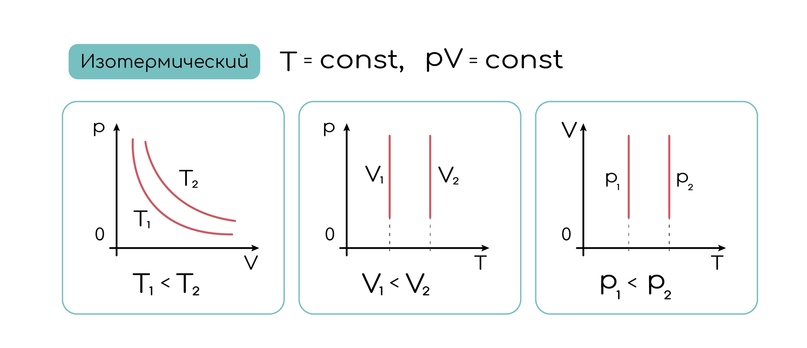
Главное помни: все это работает при постоянной массе газа, ни добавлять другие, ни убирать этот нельзя, тогда состояние будет уже другого количества газа. А формулы начала, надеюсь, ты уже выучил.