Заряженные частицы в магнитном и электрическом поле

Всем приветики! Сегодня мы с вами разберемся с комбинацией двух тем. Мы уже с Вами знаем, как магнитное поле действует на заряженную частицу, движущуюся в нем, и также знаем про то, как электрическое поле действует на заряженные частицы.

Ну давайте немного освежим память. И начнем с магнитной составляющей. На движущиеся заряженные частицы в магнитном поле действует сила Лоренца и вычисляется она по формуле ниже.

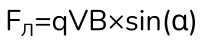
Теперь посмотри на электрическую составляющую. Чтобы определить силу, с которой электрическое поле действует на заряженную частицу можем воспользоваться формулой электрической силы.

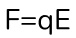
Но зачастую, магнитные поля связаны с электрическими и именно поэтому нам нужно научиться анализировать движение заряженных частиц сразу в обеих средах. Ну и на такой случай у нас есть очень крутая формула, которая называется “Обобщенная сила Лоренца”.

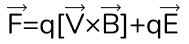
Ну, на самом деле, для нас тут ничего нового нет. Эта формула просто связывает магнитную и электрическую компоненты. Давайте же разберемся на практике, как устроены задачи на эту тему.

Условие задачи:

Электрон попадает в электромагнитное поле, как показано на рисунке. Вектор напряжённости электрического поля направлен горизонтально вправо. Вектор магнитного поля направлен от наблюдателя. Определите, при каких значениях напряжённости электроны, вылетевшие с максимально возможной скоростью, отклоняются вправо. Скорость электрона, при попадании в область магнитного и электрического поля, равна 240 км/с. Магнитная индукция поля 0,5 Тл.

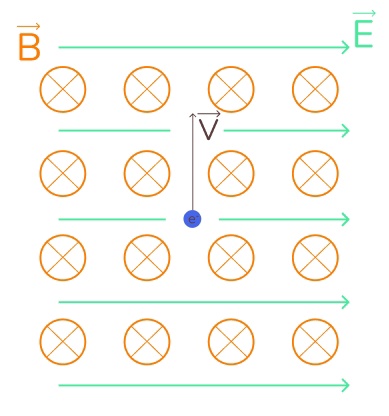
Итак, самый распространенный сценарий для нас – это взаимно обратные направления силы Лоренца и электрической силы. То есть электрическая сила в нашем случае будет направлена влево, а сила Лоренца – вправо.

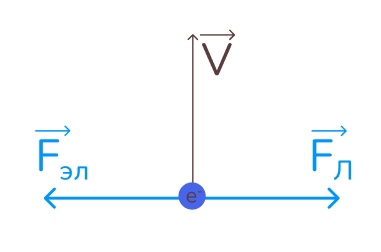
Как же мы определили направления? Для силы Лоренца пользуемся правилом левой руки, то есть:

• 4 пальца – по направлению скорости
• Линии магнитной индукции – в ладонь
• Отогнутый большой палец показывает обратное направление силы Лоренца, так как частица заряжена отрицательно

Для электрической силы мы сначала анализируем электростатическое поле. Электростатическое поле всегда направлено от “плюса” к “минусу”, то есть слева рисунка находится положительный заряд, а справа – отрицательный. Электрон, так как заряжен отрицательно, будет притягиваться к плюсу, то есть влево.

Ну и теперь мы понимаем, что нам нужно, чтобы частица отклонилась вправо по условию задачи нужно, чтобы сила Лоренца была больше, чем электрическая сила. Запишем это в виде неравенства:

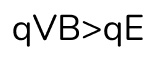
На заряд можем сократить и получим лаконичную формулу.

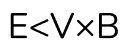
Подставляем числа:

Ответ: электрон начнет отклоняться вправо при значениях напряженности электрического поля меньше, чем 120 кВ/м.