Сила Лоренца, её направление и величина. Правило левой руки

Всем привет! Сегодня мы с вами продолжаем разбираться с магнетизмом. Тема сегодня легкая, поэтому разберем ее быстро. На очереди у нас сила Лоренца. Давайте же познакомимися с этим загадочным зверем.

Сила Лоренца — сила, которая действует на движущиеся заряженные частицы в магнитном поле. То есть если у вас есть, например, протон или электрон и он будет двигаться в магнитном поле, то на него будет действовать сила Лоренца.

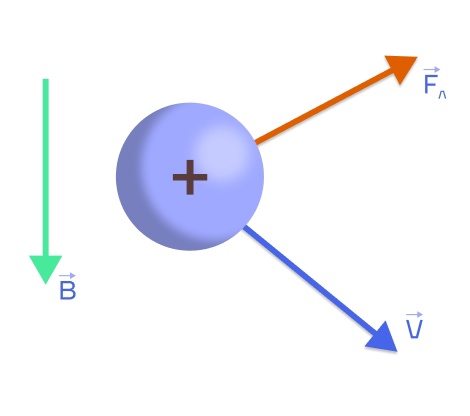
Нам здесь важно понимать то, как можно рассчитать эту силу. И вот формула для ее расчета:

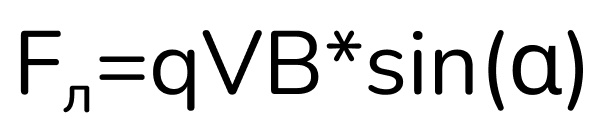
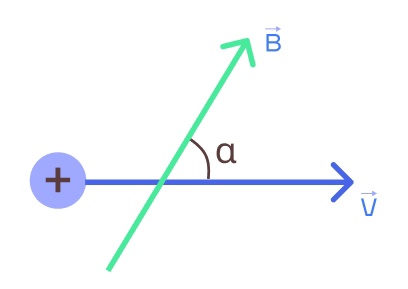
Как запомнить эту формул? Очень легко! ЛОРЕНЦ КоВБоя СЫН. Это мнемоническая формула для запоминания силы Лоренца. Угол α – это угол между направлением вектора скорости и вектором магнитного поля.

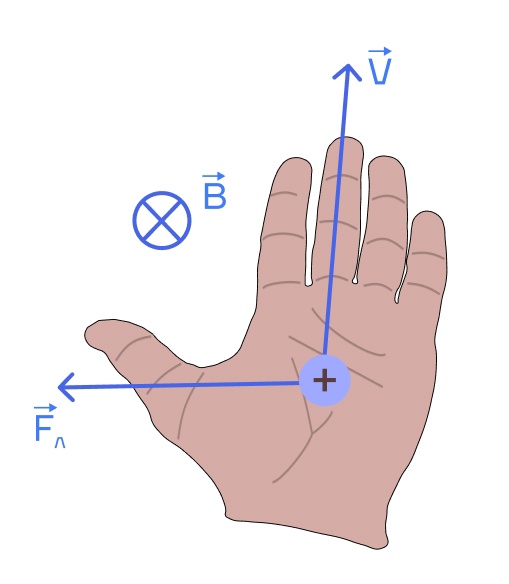
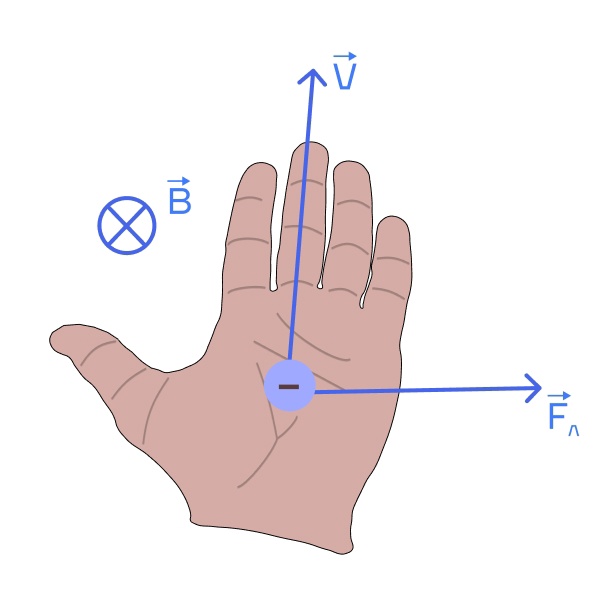
Так как сила — это векторная величина, то нам следует понимать как определить ее направление. И тут нам на помощь спешит наша левая рука. Левую руку нужно расположить таким образом, чтобы

• Линии магнитного поля входили в ладонь
• 4 пальца смотрели по направлению вектора скорости
• Отогнутый большой палец показывает направление силы Лоренца

Но это работает только для положительно заряженных частиц.

Что же делать с отрицательно заряженными частицами? На самом деле все тоже самое, просто в конце направление силы меняем на противоположное, как показано на рисунке ниже.

Если вы подумали, что это все, то вы практически правы. Осталось разобраться с траекторией заряженной частицы. Начнем с самого просто случая.

1) Угол между вектором скорости и вектором магнитной индукции равен 0. То есть заряженная частица летит параллельно магнитному полю. Если мы вспомним формулу силы Лоренца и увидим там sin(α), то сразу же поймем, что sin(0)=0. То есть сила Лоренца в этом случае равно нулю и она просто не действует на заряженную частицу и она не меняет свою траекторию и летит по прямой.

2) Если же угол между вектором скорости и вектором магнитной индукции равен 90°, то давайте разбираться. Согласно правилу левой руки, вектор скорости будет перпендикулярен вектору силы Лоренца. То есть ускорение, вызванное силой Лоренца будет перпендикулярно скорости в любой момент времени, а это значит, что такое ускорение никак не будет влиять на модуль скорости (частица будет двигаться равномерно). Но это ускорение будет менять направление скорости и частица будет двигаться равномерно по окружности.

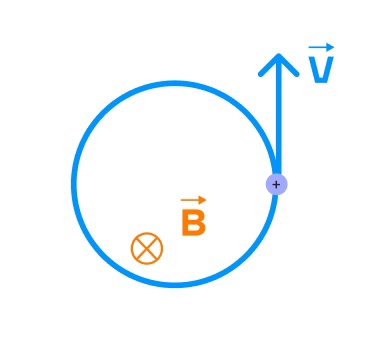
3) И теперь перейдем к самому сложному случаю. Это угол отличный от 0, 90° и 180°. В этом случае частица будет двигаться по винтовой траектории. Почему же так? Дело в том, что мы вектор скорости можем разложить на две компоненты, одна из них будет параллельна вектору магнитной индукции,а другая перпендикулярна ему. Вот и получается, что в одном направлении частица движется по прямой, как в первом случае, а в другом направлении получается, что частица движется по окружности, как во втором случае.

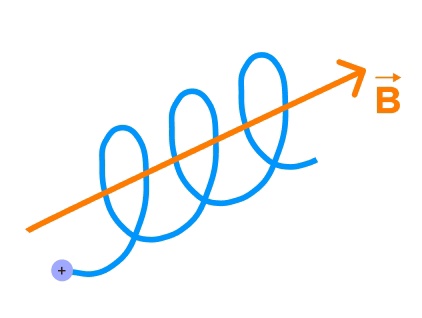
Ну и давайте под конец разберем самый распространенный случай применения силы Лоренца.

Вот условие задачи:
Электрон движется в однородном магнитном поле индукцией В=4 мТл перпендикулярно линиям магнитного поля. Найти период Т обращения.

Поскольку электрон движется перпендикулярно вектору магнитной индукции, значит он движется по окружности. А так как он движется по окружности, то на него должно действовать центростремительное ускорение, вызванное какой-то силой. Но мы ту уже с вами знаем, что это сила Лоренца заставляет двигаться частицу по окружности. Давайте воспользуемся вторым законом Ньютона:

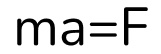
Используем формулу силы Лоренца:

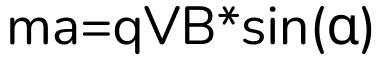
Подставим формулу центростремительного ускорения и вспомним, что sin(90°)=1:

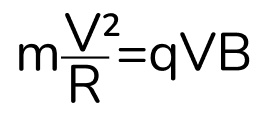
Выразим скорость частицы:

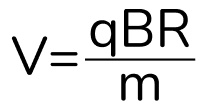
Теперь воспользуемся формулой периода обращения (это время, за которое частица пройдет путь, равный длине окружности двигаясь со скоростью V):

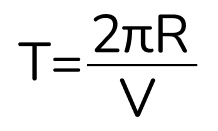
Подставим значение скорости:

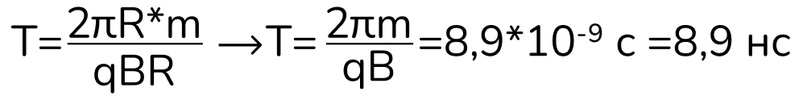
Ответ: 8,9 нс.

Кстати говоря, мы сделали очень приятный вывод, что период обращения не зависит от скорости движения частицы, а определяется только величиной магнитного поля, массой частицы и ее зарядом.