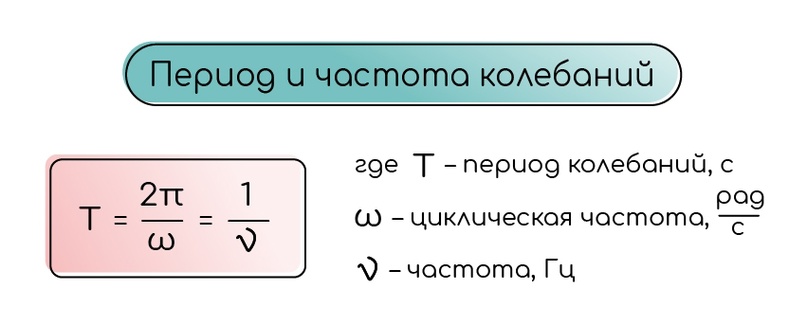
- Умный справочник
- Физика
- Гармонические колебания. Нитяной и пружинный маятник
Гармонические колебания. Нитяной и пружинный маятник
Существует несколько видов механического движения в зависимости от характера скорости: равномерное и неравномерное. Неравномерное движение может быть равнопеременным (равноускоренным или равнозамедленным). Помимо равнопеременного выделяют колебательное движение.
Колебания очень часто встречаются в жизни. Так, колеблются крылья (насекомых, самолёта), качели, камертон, сердце (даже курсы валют и твоё настроение тоже совершают колебания).
Колеблющиеся тела могут двигаться по-разному в зависимости от формы траектории: криволинейно и прямолинейно, с большим отклонением от положения равновесия или с небольшим, количество колебаний в единицу времени для каждого тела также отличается.
Но у всех колеблющихся тел есть нечто общее: движение колеблющихся тел повторяется спустя некоторый определённый промежуток времени.
Механические колебания представляют собой повторяющиеся через одинаковые промежутки времени движения, во время которых тело многократно в разных направлениях проходит положение равновесия.
Система совершает свободные (собственные) колебания, если она выведена из положения равновесия, а затем колеблется под действием внутренних сил. В реальности свободные колебания всегда затухающие.
Вынужденные колебания — это колебания, совершаемые системой под действием внешней вынуждающей силы F(t), которая изменяется во времени.
Автоколебания, как и вынужденные колебания, поддерживаются за счёт внешних сил, при этом сама колеблющаяся система задаёт (подключает) эти воздействия. Примеры автоколебательных систем: маятниковые часы с анкерным ходом, сердечно-сосудистая система, двигатели внутреннего сгорания.

Часы на Спасской башне Кремля представляют собой автоколебательную систему
Положение колеблющегося тела определяется координатой x. Положению равновесия отвечает значение x = 0. Важно определить функцию x(t), посредством которой можно описать координату тела в любой момент времени.
И в природе, и в технике распространены гармонические колебания. Гармонические колебания происходят под действием силы, которая пропорциональна смещению точки, совершающей колебания. Эта сила направлена противоположно смещению.
Для математического описания колебаний используют периодические функции — функции синуса или косинуса. Из функции синуса можно получить функцию косинуса при сдвиге аргумента на π/2 и наборот. В формулах будем использовать синус.
Гармонические колебания — это периодические изменения во времени физической величины, происходящие по закону синуса или косинуса. Координату колеблющего тела можно найти по формуле:
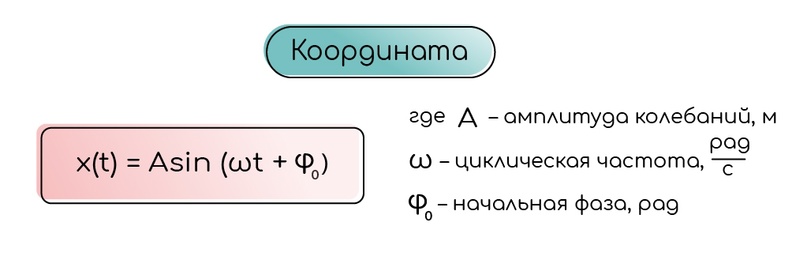
Амплитуда колебаний — это наибольшее смещение из положения равновесия.
Наглядно амплитуду можно увидеть на графике гармонического колебания:
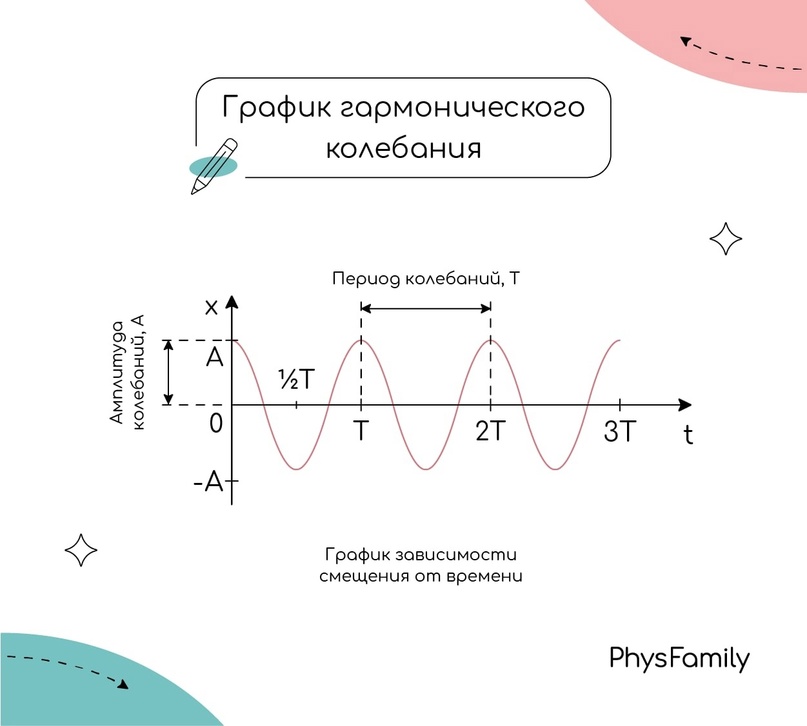
Циклическая частота показывает количество оборотов за единицу времени, выраженное в радианах. Циклическая частота характеризует скорость изменения фазы колебаний, так как чем больше циклическая частота, тем быстрее меняется фаза.
Фаза колебаний — это величина φ, которая явлется аргументом синуса, то есть стоит в уравнении координаты в скобочках, иными словами, φ = ωt + φ₀. Значение фазы при t = 0 равно φ₀ и называется начальной фазой. Начальная фаза отвечает начальной координате тела: x₀ = Asin(φ₀). Обычно фаза измеряется в радианах. Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию.
Скорость колеблющегося тела есть производная от уравнения координаты. Скорость меняется следующим образом:
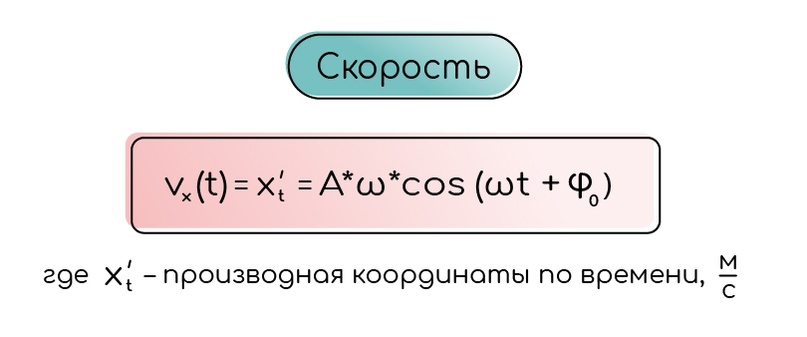
Ускорение колеблющегося тела есть вторая производная от координаты или первая от скорости, ей формула приведена ниже:

Закон сохранения энергии соблюдается для незатухающих колебаний. Как понять, что колебания незатухающие? Незатухающие колебания происходят с постоянной амплитудой.
Формула для пружинного маятника выглядит следующим образом:
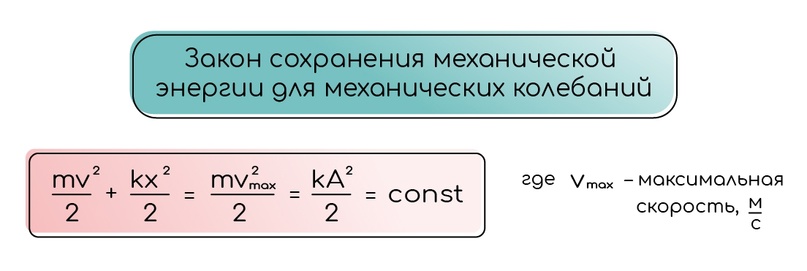
Кинетическая энергия маятника зависит от его массы и скорости, потенциальная энергия — от жёсткости и сжатия/растяжения пружины, поэтому в формуле выше на первом месте кинетическая энергия, а на втором - потенциальная.
А теперь поговорим о маятниках.

Период колебаний пружинного маятника зависит от других характеристик.

Я называю формулу периода колебаний пружинного маятника «два пирожка из мака» или «два пирожка с маком», чтобы ребятам было проще её запомнить.
Таким образом, если мы увеличиваем массу груза пружинного маятника, то период его колебаний возрастает, равно как и при уменьшении жёсткости пружины. Но зависимость не прямая: если масса выросла в 2 раза, то период увеличится только в корень из двух раз.
А ещё не забываем про связь периода и частоты колебаний: они имеют обратную зависимость, то есть при увеличении массы груза и/или при уменьшении жёсткости пружины частота уменьшается.