Импульс. Закон сохранения импульса тела

Импульс тела — векторная физическая величина. Обозначается он маленькой буквой p (да, как и давление, но спутать буквы нельзя, так как давление — скалярное). Почему буквы одинаковые? На английском языке импульс — momentum, но буква m используется для массы. А вот на немецком импульс - это der Impulse. Букву I используют для момента инерции, поэтому выбрали p.

Формула импульса:

Импульс тела прямо пропорционально зависит от массы тела и его скорости. Скорость является векторной физической величиной (равно как и импульс), а потому импульс и скорость тела всегда сонаправлены, то есть направлены в одну сторону. У импульса простая единица измерения: скорость измеряется в СИ в м/с, а масса в кг, поэтому импульс измеряется в кг·м/с. Если тело массой 1 кг движется со скоростью 1 м/с, то его импульс равен 1 кг·м/с. В русском языке импульс иногда называют количеством движения. До открытия импульса в науке использовалась теория импетуса (impetus — «толчок»).

Импульс тела и импульс силы:

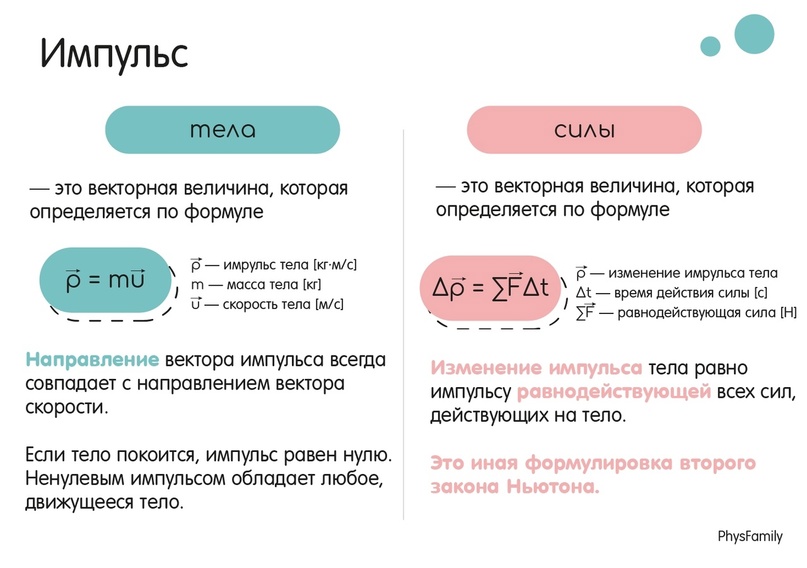
Существует также импульс силы. Если на тело действуют силы (сила), то импульс тела будет изменяться на величину, равную произведению равнодействующей этих сил на время её действия. Если силы, действующие на тело, компенсируют друг друга, то у тела отсутствует ускорение. Значит, оно будет двигаться равномерно и прямолинейно, его скорость меняться не будет, а потому импульс останется постоянным.

Вывод импульса силы

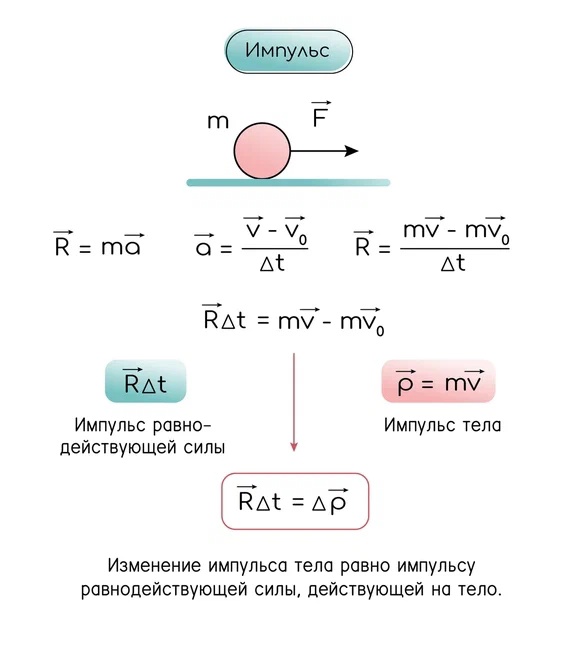
Обозначение равнодействующей сил

Равнодействующая сил — векторная сумма всех сил, действующих на тело, результирующая сила. Она может обозначаться разными буквами (R, ∑F, F), что заметно из рисунков выше. Я обозначаю равнодействующую как R. Равнодействующая сил равна скорости изменения импульса тела.

Импульс системы материальных точек

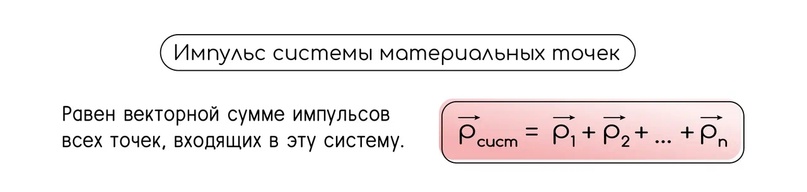
Скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе.

Про внешние силы

Все тела, которые не входят в систему материальных точек, можно назвать внешними. Внешними будут и силы, с которыми внешние тела действуют на тела системы.

***

Как находить импульс системы тел

Рассмотрим конкретное задание из ЕГЭ.

Найти импульс системы тел можно 2 способами: графическим и расчётным. Вторым способом необходимо по теореме Пифагора найти импульсы тел а и b, а затем снова использовать теорему Пифагора для нахождения модуля импульса системы.

Графический способ:

Графическим способом необходимо сложить векторы. Складывать векторы можно по правилу треугольника или правилу параллелограмма. На рисунке выше сложение правилом параллелограмма.

Складываем мы векторы импульсов тел. Суммарный импульс (импульс системы тел) равен диагонали параллелограмма, построенного на импульсах этих тел. Между правилами треугольника и параллелограмма нет различий, но в физике чаще используется правило параллелограмма.

Чаще оно используется, потому что обычно векторы приложены в одной точке.

Столкновение тел (удары)

Под столкновением или ударами понимают кратковременное взаимодействие тел. При столкновении возникают такие большие силы, что другими силами можно пренебречь.

Соударяющиеся тела как изолированная система

Если тела системы действуют друг на друга большими силами, которые по модулю во много раз больше внешних сил, то соударяющиеся тела считаем изолированной системой. Поэтому при всех видах удара будет сохраняться импульс системы, причем в векторном виде.

Если внешние силы заметны

Приведу несколько примеров. Возьмём шарики, висящие на нитях, между которыми находится лёгкая пружина, которую пережигают. Шарики необязательно должны висеть на нитях, они могут и падать в воздухе. Другой пример - шарик сталкивается с бруском, неподвижно висящим на прочной нити или шарик, висящий на нити, могут отвести из положения равновесия, затем отпустить, а в положении равновесия он столкнётся с бруском. Во всех этих случаях внешние силы направлены по вертикали, сохраняется только горизонтальная составляющая импульса системы этих тел.

В обосновании 30 задачи часто используют эту теорию.

***

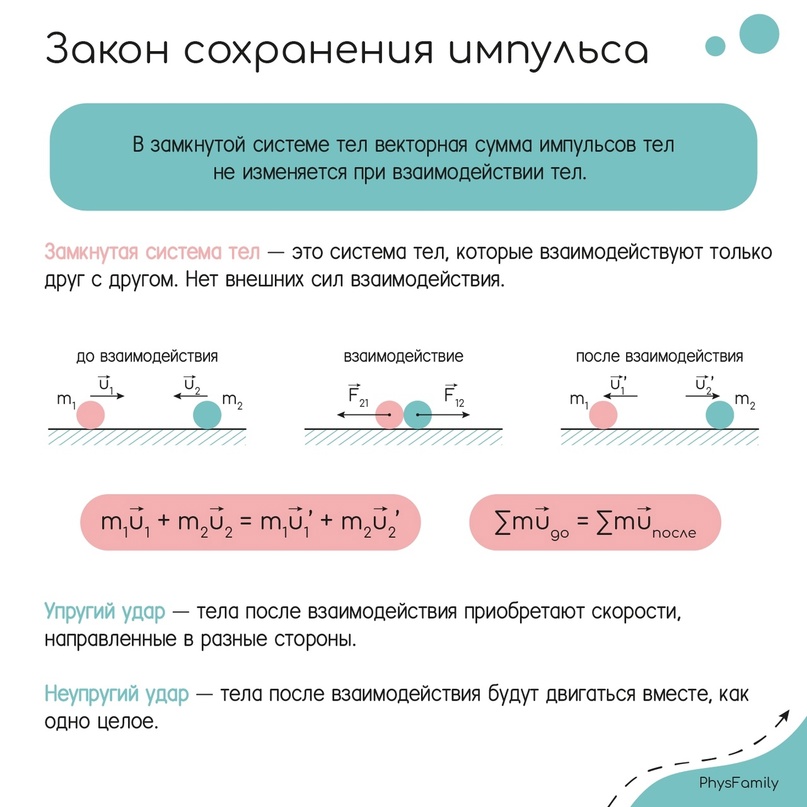
Закон сохранения импульса при абсолютно упругом и неупругом ударе

Столкновения принято разделять на центральные и нецентральные:

Центральное столкновение — столкновение, при котором векторы скоростей до удара направлены по прямой, соединяющей центры масс тел. В ЕГЭ столкновения являются центральными.

1) Абсолютно упругий удар — удар, при котором общая механическая энергия системы сохраняется. Тела после удара движутся отдельно, их скорости ищем через законы сохранения импульса и механической энергии.

2) Абсолютно неупругий удар — удар, после которого тела движутся с одинаковой скоростью, как единое целое. При этом виде удара механическая энергия неизбежно теряется (превращается в тепло и таким образом переходит во внутреннюю).

3) Для описания взаимодействия тел № 1 и № 2 используем закон сохранения импульса системы тел. Он выполняется в инерциальной системе отсчёта, если сумма внешних сил, приложенных к телам системы, равна нулю. В данном случае проекции внешних сил на горизонтальную ось в момент взаимодействия равны 0. Закон сохранения импульса в проекциях на эту ось смело можно использовать в решении задачи.

4) При разрыве снарядов в воздухе мы не знаем, в каком направлении будут двигаться осколки после разрыва, не можем считать, что они будут двигаться горизонтально, утверждать о том, что проекция силы тяжести на эту ось равна 0. Тогда считаем время разрыва снаряда малым. За малое время разрыва импульс каждого из осколков меняется на конечную величину за счёт больших внутренних сил, разрывающих снаряд при взрыве. По сравнению с ними конечная сила тяжести мала.

А вот, как выглядит идеальное обоснование к 30 задаче на импульс с точки зрения ФИПИ согласно демонстрационной версии 2023:

1. Систему отсчёта, связанную с Землёй, будем считать инерциальной.

2. Тела считаем материальными точками.

3. Для описания взаимодействия пули и шара использован закон сохранения импульса системы тел. Он выполняется в инерциальной системе отсчёта, если сумма внешних сил, приложенных к телам системы, равна нулю. В данном случае проекции внешних сил (силы тяжести и силы натяжения нити) на горизонтальную ось в момент взаимодействия равны нулю. Следовательно, можно использовать закон сохранения импульса в проекциях на эту ось.

Далее пишут про закон сохранения энергии и про условие полного оборота с минимальной скоростью, но это мы обсудим в других статьях.