Прямолинейное равноускоренное движение (ПРУД) и его сравнение с равномерным движением

Виды механического движения по скорости

По характеру скорости выделяют три вида механического движения, сегодня поговорим о каждом, но особое внимание уделим двум из них: прямолинейному равномерному и равнопеременному (равноускоренному).

Уже из названия можно понять их разницу: первое происходит с постоянной скоростью, то есть без ускорения, когда его нет (ускорение — ноль, дырка), а при втором движение происходит с постоянным ускорением, отличным от нуля.

При равномерном движении тело проходит равные расстояния за любые равные промежутки времени, при равноускоренном постоянным остаётся ускорение.

Про ускорение

Формула

где a — ускорение, v₀ — скорость в начале, v — скорость в конце рассматриваемого участка, t — время, за которое происходит это изменение скорости.

Помни: если движение с торможением, ускорение отрицательно.

Ускорение является векторной физической величиной (то есть помимо значения имеет ещё и направление), а характеризует (показывает) ускорение быстроту изменения скорости.

Простыми словами ускорение — это скорость изменения скорости.

Ускорение при прямолинейном равномерном движении равно нулю, при прямолинейном равноускоренном движении постоянно и отлично от нуля.

***

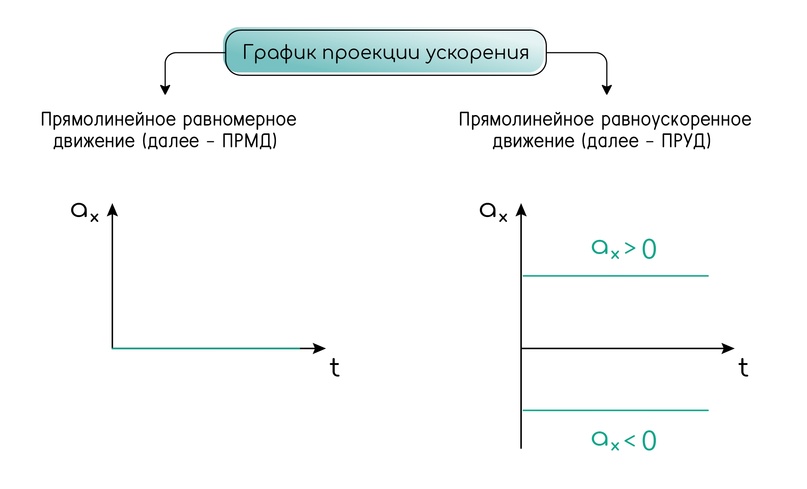
Графики ускорения

Графиком зависимости ускорения от времени и при равномерном, и при равноускоренном движении являются горизонтальные прямые линии, так как в обоих случаях ускорение постоянно. Разница лишь в том, что при равномерном движении горизонтальная прямая лежит вдоль оси времени, а при равноускоренном она находится ниже или выше оси времени.

Пример задания из открытого варианта ЕГЭ-2021:

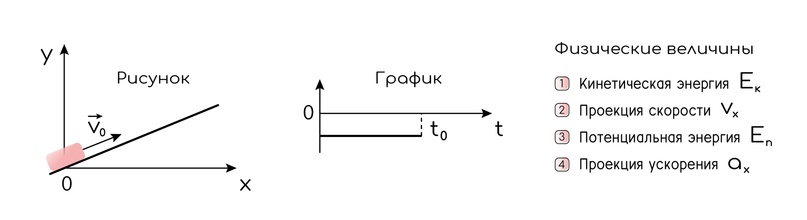
После удара шайба начала скользить вверх по гладкой наклонной плоскости со скоростью v₀ как показано на рисунке. В момент t₀ шайба возвращается в исходное положение. Установите соответствие между графиком и физической величиной, изменение которой со временем этот график может отображать.

Решение:

1. Внимательно исследуем рисунок. Шайба скользит вверх по наклонной плоскости, она будет тормозить, а в конечном итоге вернётся в начальное положение.

2. Раз шайба будет тормозить, то скорость будет уменьшаться. От скорости зависит кинетическая энергия. Потенциальная энергия зависит от высоты, то есть оба вида энергии будут изменяться в процессе движения шайбы. А вот проекция ускорения отрицательна и постоянна, ответ 4.

 

Ещё пример:

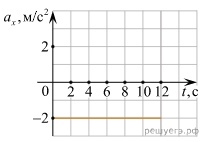
На рисунке изображён график зависимости проекции aₓ ускорения точечного тела, движущегося по гладкой поверхности, от времени t. В момент времени t = 5 с проекция скорости этого тела на ось OX равна 10 м/с. Чему был равен модуль скорости этого тела в момент начала движения при t = 0?

Решение:

Из графика следует, что проекция ускорения равна аₓ = - 2 м/с², из условия, что vₓ = 10 м/с, t = 5 c. Из формулы ускорения аₓ = (vₓ - v₀ₓ) ÷ t выразим v₀ₓ : v₀ₓ = vₓ - аₓ × t =10 - (- 2) × 5 = 20 м/с.

 

***

Про скорость

Формула

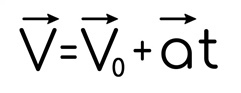
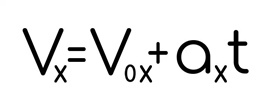
где vₓ и v₀ₓ говорит о том, что скорости рассматриваются относительно какой-то прямой, а если более научно, это проекции на ось X. Хотя в ряде задач второй части это не играет большую роль и индексы икс это бюрократия, без которой можно обойтись.

Проекция скорости выводится из формулы ускорения. Однако найти скорость по этой формуле можно только при ПРУД, если известна начальная скорость и ускорение тела. Для ПРМД (то есть когда проекция ускорения равна нулю) формула имеет больше философский смысл — из неё следует, что проекция скорости в любой момент времени равна проекции начальной скорости тела.

***

Графики скорости

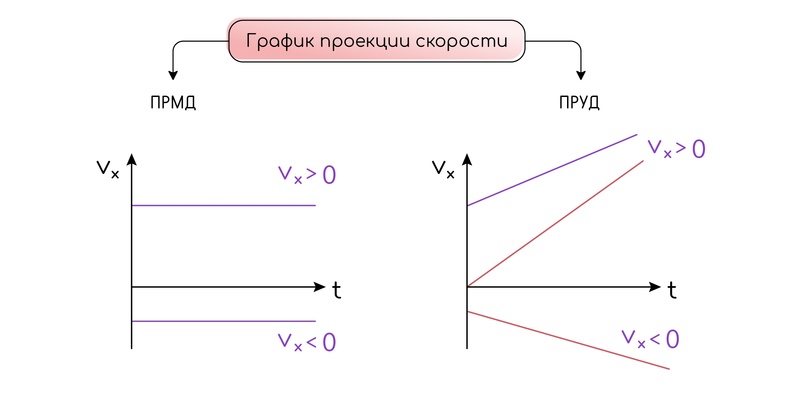
Графиком зависимости скорости от времени и при равномерном, и при равноускоренном движении являются прямые линии (графики ускорения также представляют собой прямые линии). При равномерном движении график скорости представляет собой горизонтальную прямую, которая находится ниже или выше оси времени. Если график находится выше оси, то это означает, что проекция скорости положительна (иными словами, тело движется в положительном направлении оси координат). Когда график ниже оси, то тело движется в противоположном направлении от направления оси.

При прямолинейном равноускоренном движении (ПРУД) скорость линейно зависит от времени, прямая идёт вверх или вниз под углом.

Площадь фигуры под графиком скорости

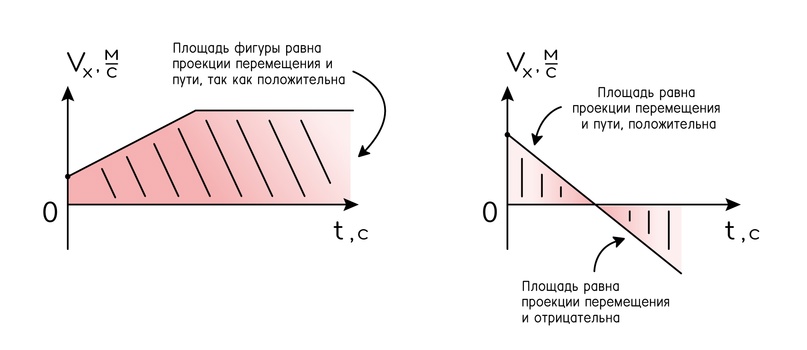
По графику мгновенной скорости (но не средней, это важно) можно отыскать много всего разного и интересного. Из очевидного: по графику скорости находится значение ускорения. Но есть и небольшой, шутка, гигантский, лайфхак: проекция вектора перемещения численно равна площади фигуры под графиком скорости. Если значения скоростей ниже нуля, то и площадь будет по знаку такой же. Помним, что проекции скорости, а значит, и перемещение могут быть отрицательными.

Относительность механического движения

(!) Скорость тела относительно неподвижной системы отсчёта равна геометрической сумме скорости тела относительно подвижной системы отсчёта и скорости подвижной системы относительно неподвижной.

Этот тезис называется законом сложения скоростей. Геометрически он осуществляется по правилу параллелограмма или треугольника. Скорость, ускорение, перемещение, путь и траекторию тела в подвижной системе отсчёта называют относительными.

Сонаправленность векторов ускорения и скорости

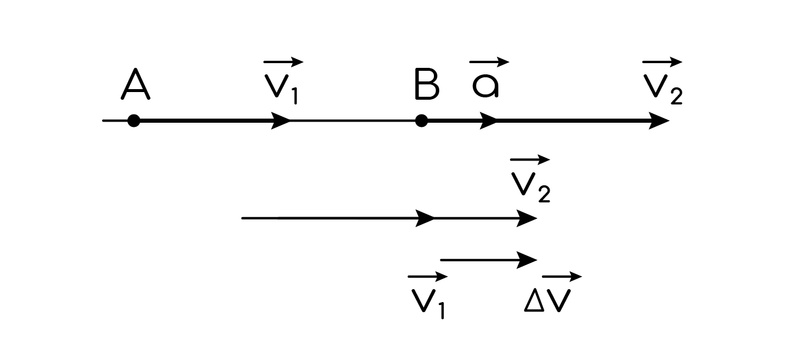
(!) Если модуль скорости уменьшается, а направление скорости не меняется, то вектор ускорения тела направлен противоположно вектору скорости.

А если модуль скорости растёт, направление не меняется, то вектор ускорения направлен в ту же сторону, что и вектор скорости (они сонаправлены).

Про перемещение

Формулы

где sₓ — проекция перемещения, в задачах второй части «иксы» можно опускать. Первая формула позволяет найти перемещение через начальную скорость, время и ускорение. По второй перемещение ищем без времени.

***

Графики перемещения

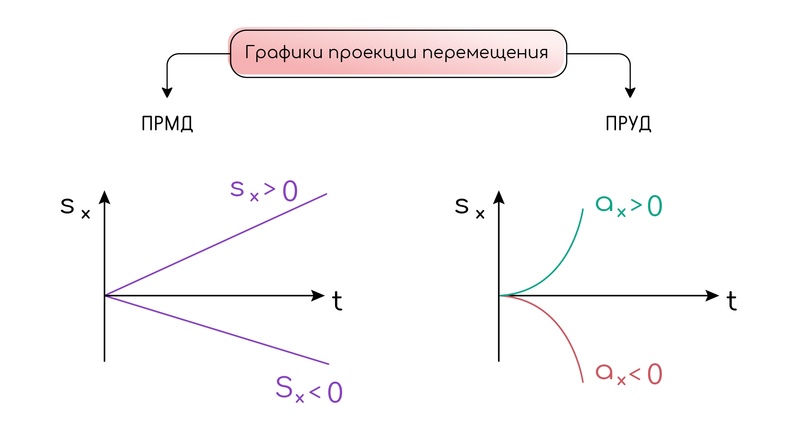
Графики зависимости проекции перемещения от времени при прямолинейном равномерном (ПРМД) и прямолинейном равноускоренном движении (ПРУД) разительно отличаются друг от друга, но тем не менее общее у них всё же имеется. Графики стартуют из начала координат.

А вот дальше идут различия. Для равномерного движения график представляет собой прямую линию, которая идёт под углом к оси времени вверх или вниз от неё. По этому графику можно найти скорость тела.

(!) За любые равные промежутки времени тело совершает одинаковые перемещения при прямолинейном равномерном движении.

Если движение равномерное, но непрямолинейное, то за каждую секунду тело может совершать разные перемещения.

Для равноускоренного движения график выглядит сложнее — он является параболой. И из его анализа можно сделать некоторые выводы:

• О знаке ускорения можно судить по веточкам параболы. Если парабола направлена ветвями вверх, то проекция ускорения положительна. Если ветви направлены вниз, то ускорение отрицательно.

(!) При прямолинейном движении вектор ускорения не всегда направлен в ту же сторону, что и вектор перемещения.

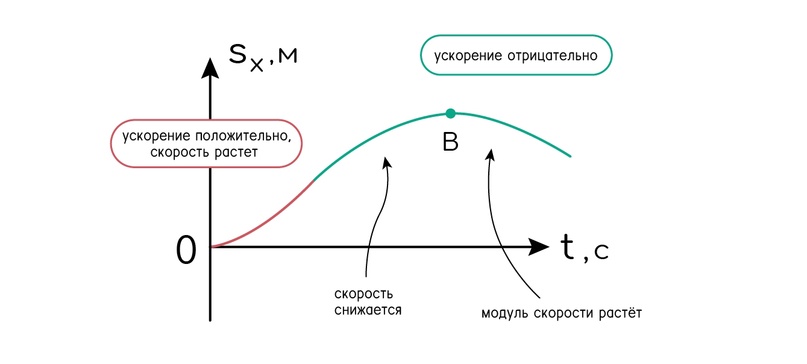
• Скорость тела — это тангенс угла наклона касательной к графику перемещения (или координаты) тела от времени, а потому если касательная к графику перемещения в какой-то точке горизонтальна, то скорость в этой точке равна нулю.

***

Поиск перемещения через график проекции скорости

По графику проекции скорости от времени можно отыскать проекцию или модуль перемещения. Причём способов два: через площадь под графиком скорости либо через одну из формул перемещения. В таком случае с графика необходимо взять значения начальной и конечной скоростей, а также высчитать ускорение.

***

Перемещение за n-ую секунду

Порой в задачах требуют найти перемещение не за четыре, семь, десять секунд, а за четвёртую, седьмую и десятую секунду. Четвёртая секунда и четыре секунды — это разные интервалы времени. Четвёртая секунда длится с третью по четвёртую секунды, то есть одну секунду между t₁=3 c и t₂=4 c, а четыре секунды охватывают время от начала отсчёта (t₀=0 c) до t₂=4 c.

У термина «перемещение» есть синоним — это «изменение координаты». Если в задаче просят найти изменение координаты за третью секунду, то это то же самое, что и перемещение в промежутке времени от двух до трёх секунд (смотри пример задания ниже).

Про путь

Формулы пути

где s, l — путь. В кодификаторе для пути есть только формула (6) без проекций.

С путём ситуация очень любопытная. В общем, мы уже обсуждали, что путь и перемещение — это разные понятия. Причём путь и перемещение могут совпадать. Так бывает, если проекция скорости в любой момент времени положительная (то есть тело двигается в направлении оси, не изменяя своего направления движения). Тогда между путём и перемещением разницы нет, и эти понятия взаимозаменяемы.

В остальных случаях проекция перемещения всегда будет меньше пути. В случае, если тело сменило направление движения, и модуль перемещения будет меньше, чем путь. В случае, если тело изначально двигалось в направлении, противоположном оси, и направление движения не меняло, модуль перемещения равен пути.

Помни, что проекция перемещения и скорость всегда совпадают по знаку, поэтому в формулах для пути есть модули в случае отрицательной скорости.

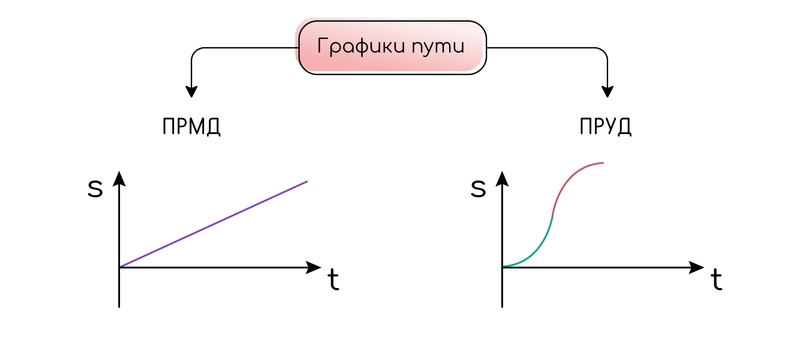
Графики пути

Путь не может быть отрицательным, а также он не уменьшается по мере движения. Поэтому графики пути для любого вида движения строго не могут быть отрицательными, а также идут упрямо вверх даже в случае смены знака ускорения, если тело разгоняется, а после тормозит. Наоборот тоже так работает.

Путь при равномерном и неравномерном движении

В равномерном и неравномерном движении работает формула:

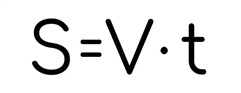
И чаще всего необходимо найти или сам путь по этой элементарной формуле, а для неравномерного движения среднюю скорость, что порой может быть весьма проблематично, ведь задач на это придумали светлые умы много. Средняя скорость – это ВЕСЬ путь, поделённый на ВСЁ время.

ВАЖНАЯ ВСТАВКА: не забывай, что физика – не математика, не шути с единицами измерения. Все переводи в систему СИ (самое важное: метры, секунды, квадратные метры, кубические метры, килограммы и т. д.)

Как правило, на ЕГЭ на эту тему идут самые простые задачи.

Путь при равноускоренном движении

Движение с постоянным ускорением значительно разнообразней и на формулы, и на графики, и на задачи.

Ты должен уметь определять по условию, какой вид движения в задаче, потому что при равноускоренном движении нельзя применять формулу равномерного.

Формула s=v*t при этом виде движения работает только для СРЕДНЕЙ скорости.

Обращай внимание на данные в задаче, если тебе сказали, что тело начинает движение, начальная скорость равна нулю, а если тело тормозит, конечная равна нулю. Напрямую в условии такое никто не даёт.

Про производные

Факт для прокаченных решал. Если ты успел пройти производные, то наверняка слышал, про физический смысл. Здесь ты можешь его увидеть наглядно. Возьми производную от пути —получишь формулу скорости:

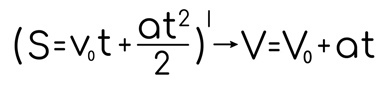
Возьми производную от скорости, получишь ускорение:

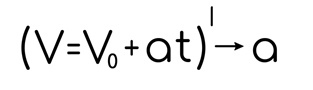
Про координату

Формулы координаты

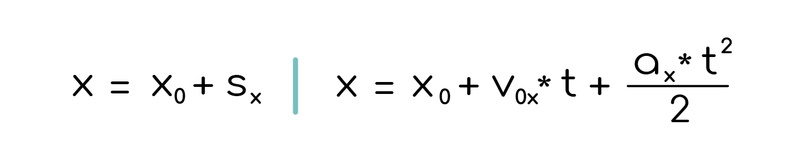
где х — конечная координата (координата в момент времени t); х₀ — начальная координата. Координата — это венец творения, её формула считается самой сложной в данном разделе, так как она самая длинная и большая. Координата зависит от начальной координаты и от перемещения, совершённого телом, что логично.

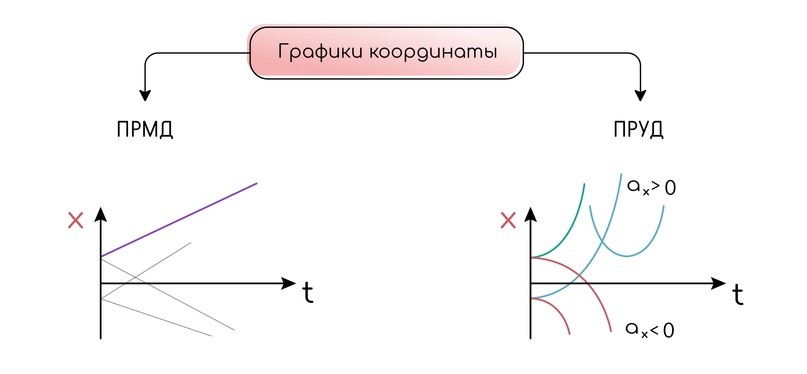
Графики координаты

Графики координаты считаются самыми мудрёными в статье. Для ПРМД (равномерного движения) график — прямая, при равноускоренном — парабола. Графики могут идти не из начала координат.