Основные определения кинематики

Место кинематики в структуре физики

Перед тем как подробно погрузиться в теорию, давай поговорим о структуре физики, так как ты чётко должен в ней разбираться, чтобы отработать задания по всем темам.

В кодификаторе выделяют 5 разделов физики: 1) Механика; 2) Молекулярная физика. Термодинамика; 3) Электродинамика; 4) Основы специальной теории относительности; 5) Квантовая физика.

В школе физику начинают изучать с механики. Она тоже непростая штучка, механика включает подразделы:

• Кинематика

• Динамика

• Статика

• Законы сохранения в механике

• Механические колебания и волны

***

Ключевое о механике

Механика — раздел физики, наука, изучающая механическое движение.

(!) Механическое движение (далее — МД) — изменение положения тела или частей тела в пространстве относительно других тел с течением времени.

Определения и фразы, отмеченные знаком (!), особенно важны — они были в сборниках ФИПИ, а значит, шанс встретить их на экзамене достаточно высок.

Механика раздаёт задачи каждому своему подразделу. Задача кинематики состоит в определении положения тела (например, его координат) в любой момент по отношению к другим телам. Кинематика абсолютно не интересуется тем, почему движение тела возникло, поэтому в данном разделе будет разбираться сам факт движения вне зависимости от причин его происхождения.

***

Основные определения кинематики

Для решения основной задачи кинематики нужна система отсчёта.

Система отсчёта — совокупность тела отсчёта, связанной с ним системы координат (далее — СК) и часов. СК нужна, чтобы измерить координаты.

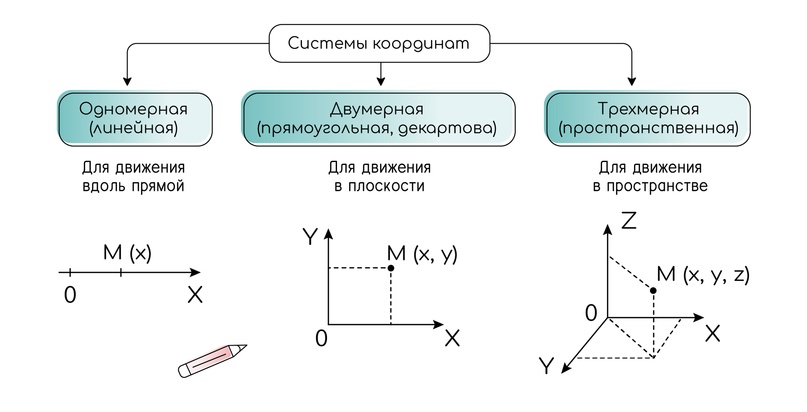
В кинематике тело мы рассматриваем как материальную точку.

(!) Материальной точкой называют тело, размерами которого в условиях данной задачи можно пренебречь.

Материальная точка имеет массу, формой тела также можем пренебречь. Модель материальной точки используют в двух случаях, о них расскажу отдельно ниже.

Последним определением, а также первой характеристикой механического движения материальной точки является траектория.

Траектория — линия, вдоль которой движется тело.

Проекция точки на ось — это основание перпендикуляра, опущенного их этой точки на данную ось.

Физические величины кинематики

К основным физическим величинам, которые изучает кинематика, относится радиус-вектор, перемещение, путь, координаты, скорость, ускорение.

Задать (описать) движение точки можно с помощью координат (координатный способ) или с помощью радиус-вектора (векторный способ).

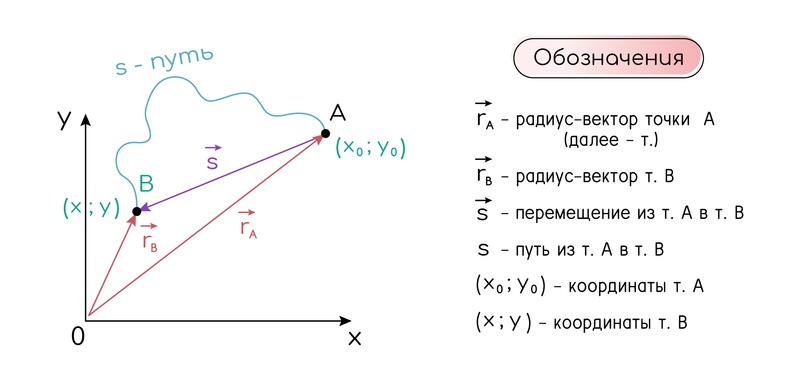
Радиус-вектор — это направленный отрезок (вектор), который соединяет начало координат и исследуемую точку.

Перемещение — вектор, соединяющий начальное и конечное положение тела.

Путь (обозначается как s или l) — длина траектории.

Важно: модуль перемещения может быть не равен пути, пройденному точкой.

Перемещение не учитывает ответвления, повороты, развороты и прочие залеты, это движение идет напрямик.

Траектория — это линия, по которой происходит движение, а путь — длина этой самой линии.

Например, тело двигалось по этой прекрасной стрелочке

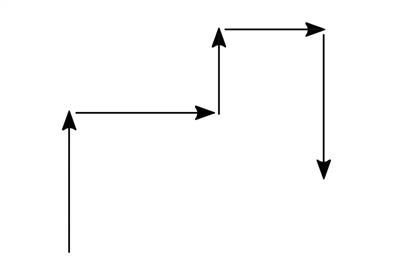
И спрашивается, где путь, а где перемещение?

СПОЙЛЕР: если ты сложишь длину всех черных стрелочек, получишь путь, а если найдешь длину зеленой стрелочки, получишь перемещение.

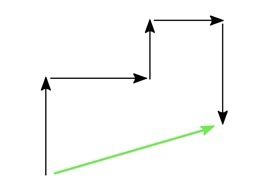
Координаты — скалярные величины, определяющие положение любой точки в пространстве.

(!) Скорость материальной точки — векторная величина, характеризующая быстроту изменения положения тела.

(!) Ускорение материальной точки — векторная величина, характеризующая быстроту изменения скорости тела. Иными словами, ускорение показывает, как быстро тело меняет свою скорость.

Классификация видов МД

Выделяют несколько классификаций видов (типов) механического движения, причём каждая классификация основана на том, как в зависимости от вида МД ведёт себя та или иная его физическая величина или характеристика.

Первая из них основана на форме траектории (прямолинейное/криволинейное).

Вторая — на характере скорости (равномерное/неравномерное/равнопеременное).

Третья выделяет виды МД в зависимости от способа перемещения (поступательное/вращательное/колебательное/сложное).

Путь и перемещение в одномерной СК

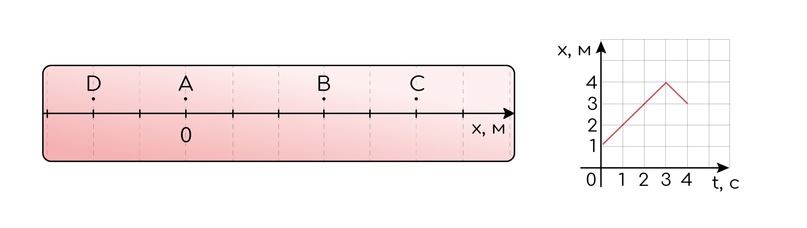
Как понять, что перед нами одномерная СК? В этом случае движение происходит по прямой, при этом для его описания достаточно одной оси — x, или y, или z. В задании на одномерную СК могут дать рисунок с координатной осью или график, например, координаты от времени.

Направим ось вправо и представим, что тело движется из т.0 сначала в т.1 налево, а затем в т.2 направо, причём конечная координата будет меньше начальной. Рисунок и формулы для расчёта пути, а также проекции и модуля перемещения будут выглядеть так:

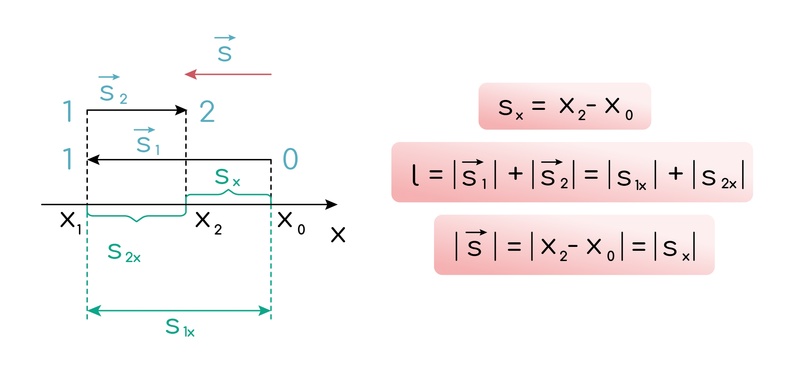
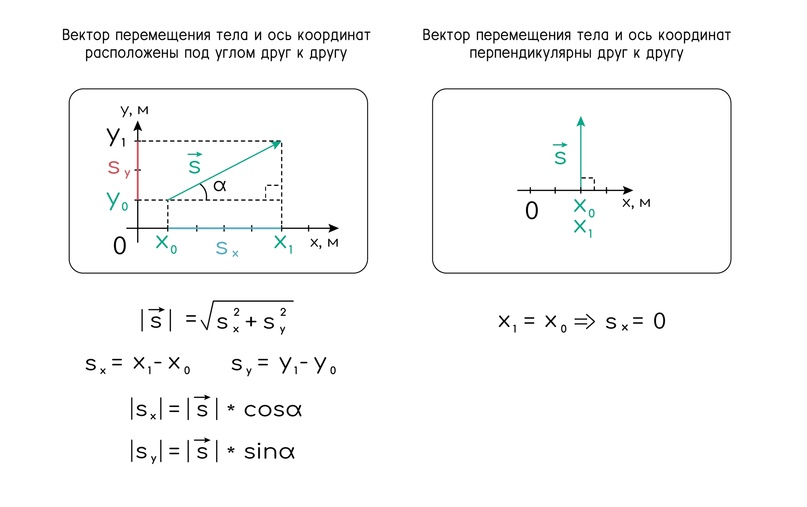
Векторы в двумерной и трёхмерной СК

В двумерной системе координат (СК) оси перпендикулярны друг другу, то есть расположены под углом 90°.

Соответственно, если нам дан вектор в двумерной СК (это может быть вектор перемещения/скорости/ускорения), то у него будет две проекции, при этом обе проекции могут быть равны нулю, если вектор нулевой (его начало и конец совпадают). Нулю может быть равна только одна из проекций, а чаще всего обе проекции выражены положительными/отрицательными числами. Для нахождения проекций работают формулы из одномерной СК.

Модуль вектора ищем по теореме Пифагора как корень из суммы квадратов проекций. В трёхмерной СК ищем корень из суммы квадратов трёх проекций.

Модуль вектора в двумерной СК через угол

Иногда в заданиях по рисунку можно найти проекции вектора на оси, а затем по теореме Пифагора найти сам модуль вектора, но порой в задании в двумерной СК изображён сам вектор, дан угол между вектором и горизонтом, значение одной из проекции, а найти надо модуль вектора. Теорема Пифагора здесь бессильна, но всегда помогут в таком случае страдания синусы и косинусы.

Напоминаю, что косинус — это отношение прилежащего катета к гипотенузе, а синус — отношение противолежащего катета к гипотенузе. Соответственно, ищем искомое через тригонометрию.

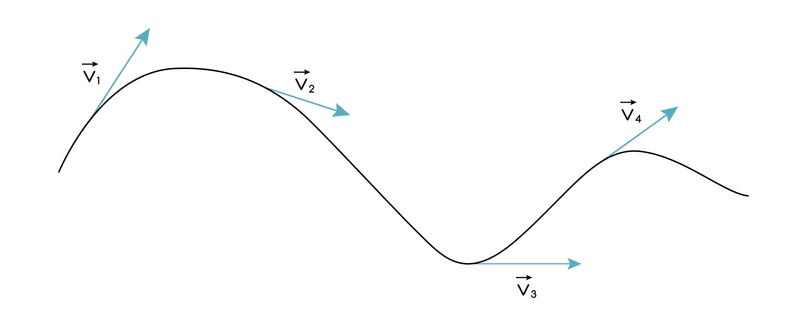
Про скорость

Вектор мгновенной скорости материальной точки всегда направлен по касательной к её траектории в сторону направления движения.

Мгновенную скорость тела можно узнать, вычислив тангенс угла наклона касательной к графику изменения координаты тела (или перемещения) от времени.

Помимо мгновенной скорости существует средняя путевая скорость, для её нахождения нужно разделить весь путь на всё время, а также модуль вектора средней скорости (чтобы его найти, делим модуль перемещения на время).

Одна из классификаций видов механического движения

Существует три вида механического движения в зависимости от характера скорости:

• равномерное, если точка за любые равные промежутки времени проходит одинаковые пути
• неравномерное
• равнопеременное (движение с постоянным ускорением, делится на равноускоренное и равнозамедленное)

Виды МД по форме траектории

Механическое движение может быть:

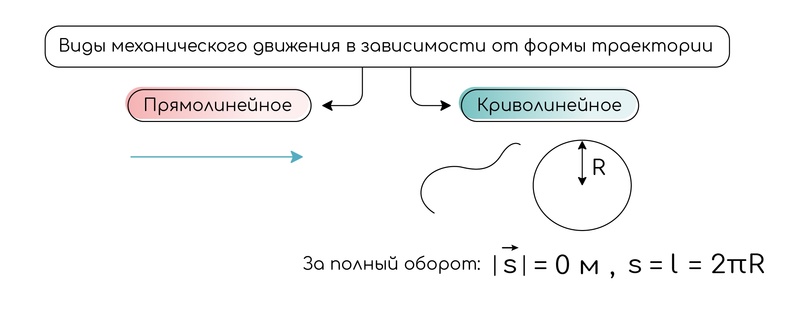
• прямолинейное, если траекторией является прямая линия

• криволинейное, если траекторией является кривая (например, винтовая линия, эллипс, гипербола, парабола, окружность)

(!) Перемещение материальной точки, движущейся по окружности, при совершении ею полного оборота равно нулю.

Виды МД по способу перемещения

Точки тела могут перемещаться по-разному — порой все точки в теле движутся одинаково, иногда — по окружностям с центром в одной точке. В первом случае движение называется поступательным, во втором — вращательным. Иногда центр масс тела движется поступательно, при этом тело вращается. Это сложное движение. А ещё тело может колебаться.

Поступательное движение

У поступательного движения есть несколько по-разному звучащих определений. Надо иметь представление о каждом.

Есть простое определение: поступательное движение — движение, при котором все точки тела в любой момент времени движутся одинаково.

Есть определение каноническое из учебника А.В.Перышкина для 9 класса: поступательное движение — движение тела, при котором прямая, соединяющая любые две точки этого тела, перемещается, оставаясь всё время параллельной своему первоначальному направлению.

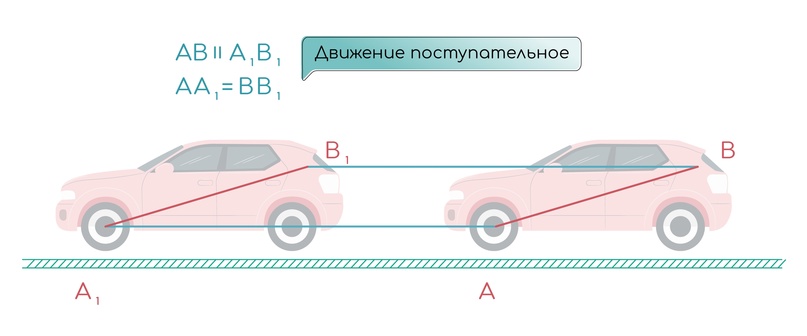
Интересно, что поступательным может быть как прямолинейное, так и криволинейное движение, то есть классификации МД дополняют друг друга. Пример — кабина колеса обозрения, она движется поступательно.

А что означает, что точки движутся одинаково? Это значит, что одинаково со временем меняются физические величины (скорость тела, путь и т. д.).

Вся эта философия необходима, чтобы принять тело за материальную точку. Ведь если все точки тела движутся одинаково, то достаточно рассмотреть движение только одной точки, при этом задачу решить проще. Тело в таком случае принимают за материальную точку, при этом его размеры даже не обязательно должны быть очень малы в сравнении с пройденным путём.

Когда считаем тело материальной точкой?

Итак, описывать тело моделью материальной точки можно в двух случаях: если расстояния, проходимые точками тела, очень велики по сравнению с его размерами, либо если тело движется поступательно независимо от его размеров и пройденного расстояния, то есть даже если они соизмеримы.