- Умный справочник
- Физика
- Векторные и скалярные величины; значения векторных величин
Векторные и скалярные величины; значения векторных величин
В чём разница?
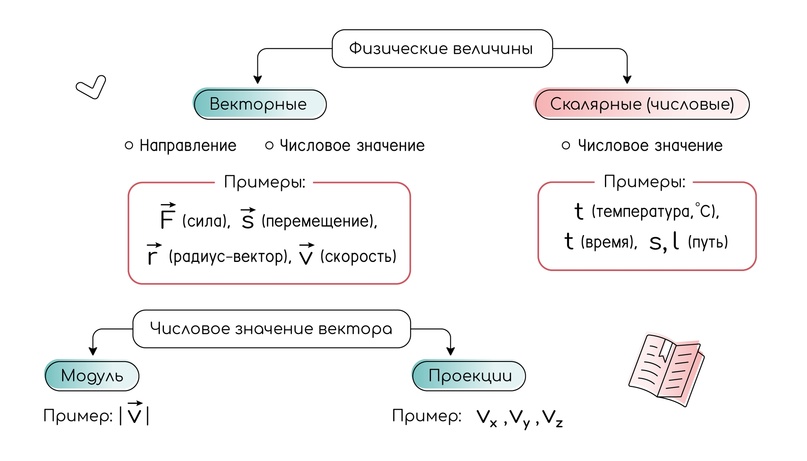
Физика исследует свойства тел, а также изучает поля (например, электромагнитные и гравитационные). Эти характеристики называются физическими величинами. Они могут быть векторными или скалярными (числовыми).
Векторные физические величины имеют направление и числовое значение. Числовое значение вектора выражается двумя способами:
1) модуль — длина вектора.
2) проекция — это длина отрезка оси, заключённого между двумя перпендикулярами, опущенными на ось из начала и конца вектора, взятая со знаком «+» или «-». Проекций всегда столько же, сколько и осей.
Скалярные физические величины имеют только числовое значение.
Чем отличается проекция вектора от модуля?
Проекция — это «след» вектора на оси. Модуль — это длина вектора.
Проекции записывают, добавив к обозначению физической величины индексы, например, Fₓ, aₓ и т. д.
Модуль можно писать по-разному: иногда ставят знак модуля, а иногда просто опускают значок вектора, подразумевая под этим модуль (например, обозначают v - модуль скорости, s - модуль перемещения, F - модуль силы).
В одномерной системе координат, если тело движется в ту же сторону, куда и направлена ось, одно и то же число может быть и проекцией, и модулем вектора.
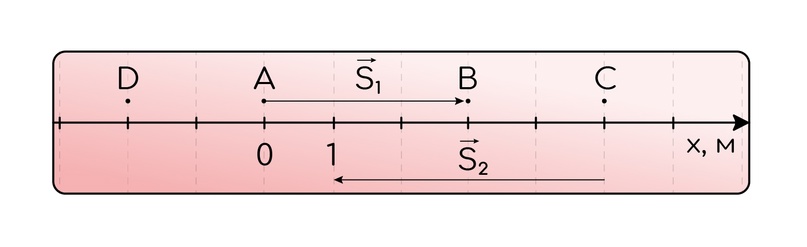
Так, модуль первого вектора перемещения равен 3 м; проекция первого вектора перемещения также равна 3 м.
А вот со вторым вектором всё не так просто: его проекция отрицательна и равна - 4 м, ну а модуль, ясное дело, положительный (равен 4 м).
В двумерной системе координат проекций всегда две (по количеству осей). Обе проекции и модуль вектора всегда образуют прямоугольный треугольник. Достаточно двух элементов в этом треугольнике, чтобы найти любой другой. Для этого тебе пригодится теорема Пифагора и (или) знание тригонометрических функций.
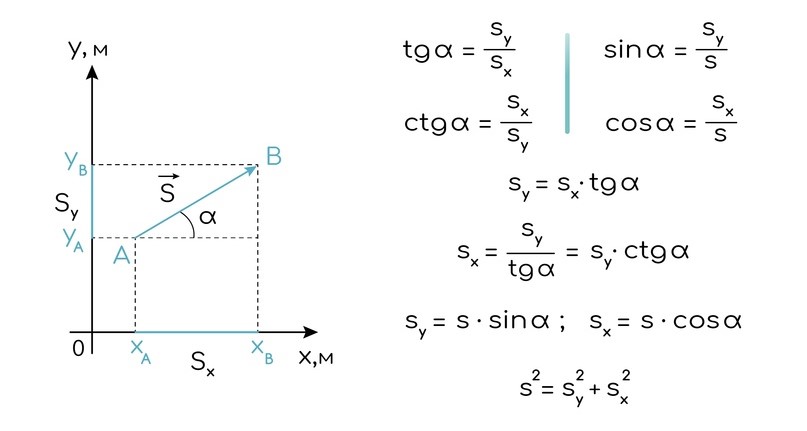
Найти проекцию вектора на ось можно с помощью:
1) модуля вектора и тригонометрической функции (синуса или косинуса);
2) проекции вектора на другую ось и тригонометрической функции (тангенса или котангенса);
3) модуля вектора и проекции вектора на другую ось.